Question: Let a. Show that is continuous at x = 0. b. Use the fact that every nonempty open interval of real numbers contains both

Let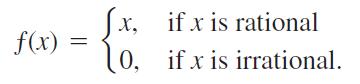 f(x) = fx, if x is rational 10, 0, if x is

a. Show that ƒ is continuous at x = 0.

b. Use the fact that every nonempty open interval of real numbers contains both rational and irrational numbers to show that ƒ is not continuous at any nonzero value of x.

f(x) = fx, if x is rational 10, 0, if x is irrational.

Step by Step Solution

★★★★★

3.40 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To show that is continuous at x 0 we need to show that the limit of the function as x approaches 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

a. Use the fact that every nonempty interval of real numbers contains both rational and irrational numbers to show that the function is discontinuous at every point. b. Is right-continuous or...

In this project you will construct an increasing function that is discontinuous at each rational point in (0, 1) and continuous at each irrational point in (0, 1). We will need two basic facts: a....

If x is a rational number, then x can be written in a unique way as a quotient of integers m/n where n > 0 and m and n have no common factors greater than 1. (We say that such a fraction is in lowest...

a. Use the fact that every nonempty interval of real numbers contains both rational and irrational numbers to show that the function f(x) = 1, if x is rational 0, if x is irrational is discontinuous...

You have to show all your work, including intermediate steps, and explain how you reached your conclusion. A. Complements and Applications 1. Consider the function f(x) = {x x rational 0 x irrational...

A function discontinuous at every point. Use the fact that between any two distinct real numbers there exist (infinitely many) rational numbers and (infinitely many) irrational numbers to show that...

r method to solve it.Look for relevant information: Identify the given information in the problem that will help you solve it. Circle or underline the numbers or variables that are important. phrases...

solve it.Look for relevant information: Identify the given information in the problem that will help you solve it. Circle or underline the numbers or variables that are important. phrases that...

solve complex problems. Apart from its applications in various fields, math has practical applications in everyday life. Basic math skills such as addition, subtraction, multiplication, and division...

cooking, and shopping. Understanding mathematical concepts such as percentages, fractions, and ratios is essential when making decisions such as buying a home, investing in stocks, or comparing...

Use (a) The Trapezoidal Rule, (b) The Midpoint Rule, and (c) Simpsons Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places) 1. T+ x* dx, n-8...

The manager of a bookstore recorded the number of customers who arrive at a checkout counter every 5 minutes from which the following distribution was calculated. Calculate the mean and standard...

What is the company's times interest earned is enter your response here times. ( Round to two decimal places. ) Balance Sheet ( $ thousands ) Cash 5 0 0 Accounts receivable 2 0 1 0 Inventories 1 0 8...

What are the business-definition aspects of KA&L (offer, target market, capability, problem solving)?

If 3 x = 3 4 , then x = _________.

In problem, determine whether the function is one-to-one. Domain Range 20 Hours $200 25 Hours 30 Hours $350 $425 40 Hours

In problem, (a) Verify that the function is one-to-one, (b) Find the inverse of the given function. {(1, 2), (3, 5), (5, 8), (6, 10)}

granite bay jet ski level 2 TRANSACTIONS FOR JUNE 17-23 June 17 On March 20 of this year, Granite Bay Jet Ski, Inc., borrowed $12,000 cash by issuing a 90-day, 11.0%, note payable. The proceeds of...

pls help fill Required information Use the following information for the Exercises below. (Algo) [The following information applies to the questions displayed below.] Simon Company's year-end balance...

Though his sales are increasing from year to year, Hugh G. Losses, President of USS Enterprises, is concerned because his competitors are stealing some of his prime customers (he is, in effect,...