Question: The double integral dx dy is an improper integral and could be defined as the limit of double integrals over the rectangle [0, t] x

The double integral 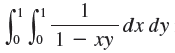dx dy — ху Jo Jo 1 dx dy is an improper integral and could be defined as the limit of double integrals over the rectangle [0, t] x [0, t] as t → 1-. But if we expand the integrand as a geometric series, we can express the integral as the sum of an infinite series. Show that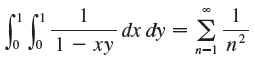 o Jo 1 — ху dx dy = E n-1 n-1 n |-|1*

dx dy Jo Jo 1 o Jo 1 dx dy = E n-1 n-1 n |-|1*

Step by Step Solution

★★★★★

3.45 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Since xy 1 except at 1 1 the formula for the ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Find the function whose exact differential is d f = cos (x) sin (y) sin (z)dx +sin (x) cos (y) sin (z)dy +sin (x) sin (y) cos (z)dz and whose value at (0,0,0) is 0. Find the area of the circle of...

Use polar coordinates to combine the sum into one double integral. Then evaluate the double integral. +*[vdv dx + f /4-2 Se S ty dy dx + ty dy dx + dy dx J1//2 J1-x2

a) Prove that the improper integral «£° e-x2 dx converges to a finite real number. b) Prove that if f is the value of the integral in part a), then c) Show that d) Let Qk represent...

Question 2: Explain geometrically how the formula for a single A is obtained. Explain why this area depends on r and not just r. Note that this is about just a single "polar rectangle" and not the...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Question 1: Summarize the Riemann sum argument that gives the formula of area as a double integral. When computing these, you might have memories of Calculus I and finding the area of regions. This...

Feedback: #1: This is not the argument in this reading passage. (0/4). Question 1: Summarize the Riemann sum argument that gives the formula of area as a double integral. Hint 1: Read the subsection...

Hello, please answer all questions (1-4) seen below and ensure that you answer everything correctly. Please do not attempt these problems if you do not understand/can't answer them properly. These...

List six characteristics of annual objectives.

Discuss the areas of factor overhead and how actual versus budget affects the bottom line of organizations. Analyze the various ways in which factory overhead is applied.

The _ _ _ compares monthly debt payments including a mortgage payment and any other loan or alimony payments to monthly gross pay. Question 2 3 options: debt payments - to - income method debt to...

Which countries outside the West have had the most development success in the last century? Are these non-Western development models useful for todays LDCs?

Find a vector a with representation given by the directed line segment AB(vector). Draw AB(vector) and the equivalent representation starting at the origin. A(2, 3), B(2, 1)

Describe and sketch the surface. yz = 4

Find a b. a = s, 2s, 3s), b = t. t. 5t

Please answer in the format requested. You wish to test the following claim (H.) at a significance level of o = 0.001. Ho:p = 52.4 Ha:u

please help me with only two questions (pictures of questions uploaded/click and see) X 9.3.67-P Question Help The value obtained for the test statistic, z, in a one-mean z-test is given. Whether the...

Consider the following information: State of Economy Probability of State of Economy Rate of Return if State Occurs Recession .16 .12 Normal .48 .14 Boom .36 .33 Required: Calculate the expected...