The Second Derivative Test for Local Maxima and Minima says: a. has a local maximum value
Question:
The Second Derivative Test for Local Maxima and Minima says:
a. ƒ has a local maximum value at x = c if ƒ′(c) = 0 and ƒ″(c)
b. ƒ has a local minimum value at x = c if ƒ′(c) = 0 and ƒ″(c) > 0.
To prove statement (a), let P = (1/2) |ƒ″(c)|. Then use the fact that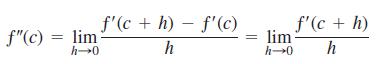
to conclude that for some δ > 0,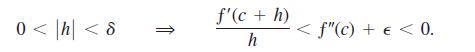
Thus, ƒ′(c + h) is positive for -δ
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
ANSWER To prove statement a we need to show that if c 0 and c 0 then has a local maximum val...View the full answer
Answered By
Chandrasekhar Karri
I have tutored students in accounting at the high school and college levels. I have developed strong teaching methods, which allow me to effectively explain complex accounting concepts to students. Additionally, I am committed to helping students reach their academic goals and providing them with the necessary tools to succeed.
0 Reviews
10+ Question Solved
Related Book For 
Thomas Calculus Early Transcendentals
ISBN: 9780321884077
13th Edition
Authors: Joel R Hass, Christopher E Heil, Maurice D Weir
Question Posted:
