Question: Consider a two-hypothesis decision problem where (a) Find the likelihood ratio Î(Z). (b) Letting the threshold n be arbitrary, find the decision regions R 1
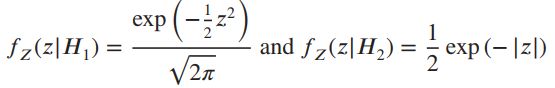
(a) Find the likelihood ratio Λ(Z).
(b) Letting the threshold n be arbitrary, find the decision regions R1 and R2 illustrated in Figure 11.1. Note that both R1 and R2 cannot be connected regions for this problem; that is, one of them will involve a multiplicity of line segments.
Figure 11.1
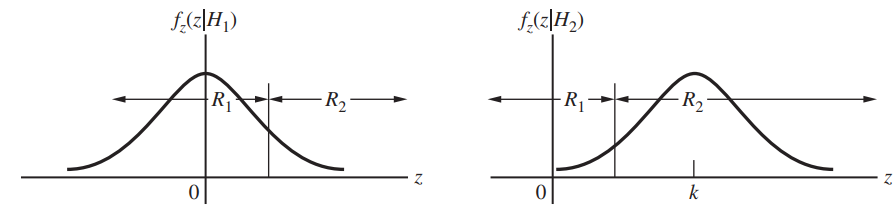
(i-) and fz(z|H2) exp = ; exp(-|z|) fz(z|Hj) = 2 f,(z|H}) f,(z\H,) R1 -R2 -R1 R2 0| k
Step by Step Solution
3.33 Rating (159 Votes )
There are 3 Steps involved in it
a The likelihood ratio is b The decision regions are determined by the set of in... View full answer

Get step-by-step solutions from verified subject matter experts


