Complete the approximation argument for Lvy's arc-sine law from (S 8.9) : a) Show, by a direct calculation, that (v_{n, lambda}(x)) converges as (n

Complete the approximation argument for Lévy's arc-sine law from \(\S 8.9\) :

a) Show, by a direct calculation, that \(v_{n, \lambda}(x)\) converges as \(n \rightarrow \infty\). Conclude from (8.16) that \(v_{n, \lambda}^{\prime \prime}\) converges.

b) Integrate the ODE (8.16) to see that \(v_{n, \lambda}(x)-v_{n, \lambda}^{\prime}(0)\) has a limit. Integrating once again shows that \(v_{n, \lambda}^{\prime}(0)\) converges, too.

c) Identify the limits of \(v_{n, \lambda}, v_{n, \lambda}^{\prime}\) and \(v_{n, \lambda}^{\prime \prime}\).

Data From Equation (8.16)

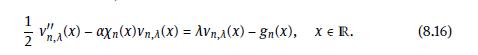
1 vn, (x) - axn(x)vn,(x) = AVn,(x)-gn(x), x = R. (8.16)