Let (left(X_{t} ight)_{t geqslant 0}) be a diffusion process with the infinitesimal generator (L=L(x, D)=left.A ight|_{mathcal{C}_{c}^{infty}}) as in (23.1). Write (M_{t}^{u}=uleft(X_{t} ight)-uleft(X_{0} ight)-int_{0}^{t} L uleft(X_{r}

Let \(\left(X_{t}\right)_{t \geqslant 0}\) be a diffusion process with the infinitesimal generator \(L=L(x, D)=\left.A\right|_{\mathcal{C}_{c}^{\infty}}\) as in (23.1). Write \(M_{t}^{u}=u\left(X_{t}\right)-u\left(X_{0}\right)-\int_{0}^{t} L u\left(X_{r}\right) d r\).

a) Show that \(M^{u}=\left(M_{t}^{u}\right)_{t \geqslant 0}\) is an \(L^{2}\) martingale for all \(u \in \mathcal{C}_{c}^{\infty}\left(\mathbb{R}^{d}\right)\).

b) Show that \(M^{f}=\left(M_{t}^{f}\right)_{t \geqslant 0}\) is a local martingale for all \(f \in \mathcal{C}^{2}\left(\mathbb{R}^{d}\right)\).

c) Denote by \(\left\langle M^{u}, M^{\phi}\rightangle_{t}, u, \phi \in \mathcal{C}_{c}^{\infty}\left(\mathbb{R}^{d}\right)\), the quadratic covariation of the \(L^{2}\) martingales \(M^{u}\) and \(M^{\phi}\), cf. (15.8) and Theorem 15.15.b). Show that \[\begin{aligned}
\left\langle M^{u}, M^{\phi}\rightangle_{t} & =\int_{0}^{t}(L(u \phi)-u L \phi-\phi L u)\left(X_{s}\right) d s \\
& =\int_{0}^{t} abla u\left(X_{S}\right) \cdot a\left(X_{S}\right) abla \phi\left(X_{S}\right) d s .
\end{aligned}\]
\(\left(x \cdot y\right.\) denotes the Euclidean scalar product and \(\left.abla=\left(\partial_{1}, \ldots, \partial_{d}\right)^{\top}.\right)\)
Remark. The operator \(\Gamma(u, \phi):=L(u \phi)-u L \phi-\phi L u\) is called carré-du-champ or mean-field operator.

Data From 15.15 Theorem 

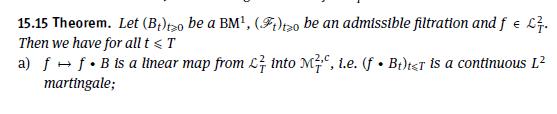
15.15 Theorem. Let (B+)to be a BM, (F)to be an admissible filtration and f = C. Then we have for all t < T a) ff. B is a linear map from into M, i.e. (f Bt)ter is a continuous L martingale;