Show that in Example 21.7 [X_{t}^{circ}=exp left(-int_{0}^{t}left(beta(s)-delta^{2}(s) / 2 ight) d s ight) exp left(-int_{0}^{t} delta(s) d B_{s} ight)] and verify the expression given for

Show that in Example 21.7

\[X_{t}^{\circ}=\exp \left(-\int_{0}^{t}\left(\beta(s)-\delta^{2}(s) / 2\right) d s\right) \exp \left(-\int_{0}^{t} \delta(s) d B_{s}\right)\]

and verify the expression given for \(d X_{t}^{\circ}\). Moreover, show that

\[X_{t}=\frac{1}{X_{t}^{\circ}}\left(X_{0}+\int_{0}^{t}(\alpha(s)-\gamma(s) \delta(s)) X_{s}^{\circ} d s+\int_{0}^{t} \gamma(s) X_{s}^{\circ} d B_{s}\right)\]

Data From 21.7 Example

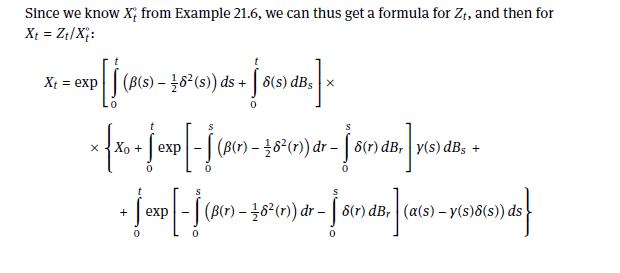
Data from 21.6 Example

21.7 Example (Linear SDES). A linear SDE is an SDE of the form dx+= (a(t) + B(t)x+) dt + (y(t) + 8(t)X+) dB+, with non-random coefficients a, , y, 8: [0, 0) R. Let X; be a random process such that 1/X is the solution of the homogeneous equation (1.e. where a = y = 0) for the initial value X = 1. From the explicit formula for 1/X of Example 21.6 it is easily seen that dx=(-(t) +82(t))X; dt - 6(t)XdBt X = exp p[- (B(s)-82(s)) ds-8(s) dBs Set Zt := X+X+; using Ito's formula (18.14) for the two-dimensional It process (Xt, X), we see dz = x+ dx + xdx+ - (y(t) + 6(t)x+)6(t)X, dt, and this becomes, if we insert the formulae for dX, and dx, dZt = (a(t) - y(t)6(t))X; dt + y(t)XdBt. Ex. 21.4