Let (B_{t}=left(b_{t}, beta_{t} ight)) be a (mathrm{BM}^{2}). Solve the (mathrm{SDE}) [X_{t}=x+b int_{0}^{t} X_{s} d s+sigma_{1} int_{0}^{t} X_{s} d b_{s}+sigma_{2} int_{0}^{t} X_{s} d beta_{s}] with (x,

Let \(B_{t}=\left(b_{t}, \beta_{t}\right)\) be a \(\mathrm{BM}^{2}\). Solve the \(\mathrm{SDE}\)

\[X_{t}=x+b \int_{0}^{t} X_{s} d s+\sigma_{1} \int_{0}^{t} X_{s} d b_{s}+\sigma_{2} \int_{0}^{t} X_{s} d \beta_{s}\]

with \(x, b \in \mathbb{R}\) and \(\sigma_{1}, \sigma_{2}>0\).

Rewrite the SDE using the result of Problem 19.3 and then apply Example 21.4.

Data From 19.3 Problem

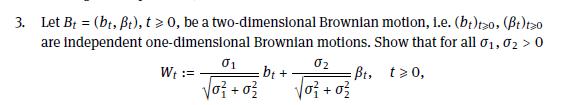
3. Let Bt (bt, t), t> 0, be a two-dimensional Brownian motion, l.e. (bt)tzo, (t)tzo are independent one-dimensional Brownian motions. Show that for all 1, 02 > 0 01 W == + :b + 02 Bt, t0, +