Question: Embedded jump chain. Let E be countable and .Xn0 a Markov chain on E with transition matrix . Let T0 D 0 and Tk D

Embedded jump chain. Let E be countable and .Xn0 a Markov chain on E with transition matrix …. Let T0 D 0 and Tk D inf¹n > Tk1 W Xn ¤ Xn1º be the time of the kth jump of .Xn0. Show that the sequence X

k WD XTk , k 0, is a Markov chain with transition matrix

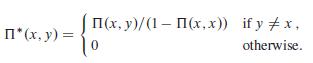
(x, y)/(1-(x,x)) if yx, I* (x, y) = 0 otherwise.

Show further that, conditional on .X
k /k0, the differences TkC1Tk 1 are independent and geometrically distributed with parameter 1 ….X
k;X
k /.

(x, y)/(1-(x,x)) if yx, I* (x, y) = 0 otherwise.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability Statistics Questions!

S Markov chains in continuous time. Let E be countable and G D .G.x; y//x;y2E a matrix satisfying the properties (i) G.x; y/ 0 for x y, (ii) a.x/ WD G.x; x/ (iii) a WD supx2E a.x/ We construct a...

Excursions from a recurrent state. Consider a Markov chain with a countable state space E and transition matrix that starts in a recurrent state x 2 E. Let T0 D 0 and, for k 1, let Tk D infn > Tk1...

Consider a discrete time Markov chain with finite or countable state space S and transition matrix II(x, y), x, y E S, so that II(x, y) > 0 is the probability for the Markov chain to jump from z to y...

1. Let Xn be a Markov chain on the state space S = {a, b, c, d, e, f } with transition matrix a b C d a 0 1/3 2/3 0 O b 2/3 0 1/3 0 0 0 C 1/3 2/3 0 0 0 0 d 0 1/6 1/6 2/3 0 e 0 0 0 1/2 0 1/2 0 0 0 0 0...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

Provide an appropriate query to show that the above program can give an incorrect result. [4 marks] (b) Explain the cause of the error. [6 marks] (c) Suggest a correction. [5 marks] (d) Write a...

3. Suppose we have an M/M/1/2 queueing system. That is, suppose customers arrive according to a Poisson process with rate > 0. There is a single server, and the service times are exponentially...

1. Consider a continuous-time Markov chain with no absorbing states. Let G be its generator matrix and R the transition matrix of its jump chain. Let x = (:12; : i E S) be a row vector of nonnegative...

s sf Define the terms opaque type and concrete type. [5 marks] The following is a shortened version of one of the definition modules described in the Modula-2 user manual: Provide a suitable...

If E (W) = and Var (W) =2, show that r(-) Var(W )- =0 and

Each of the following reactions has been reported in the chemical literature and gives a single organic product in high yield. Write the structure of the product for each reaction. (a)...

When Elijah invests in a bond that cannot be paid when it is due, he should have been concerned with _ _ _ _ _ before he made his investment. inflation risk interest - rate risk market risk credit...

Consider a completely randomized design with k treatments. Assume all pairwise comparisons of treatment means are to be made using a multiple comparisons procedure. Determine the total number of...