Apply the variational method (Approximation 3 ) to the case in exercise 2.

Data From Exercise 2:-

Consider a helium atom with two electrons in the \(n=2, l=0\) state. Calculate their ground state, using the two approximations in the text.

Data From Approximation 3:-

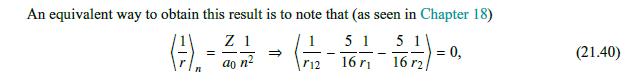
We can use a variational method to account for the fact that, when considering the interaction of the individual electrons with the nucleus, the electrons do not see the full charge +Ze of the nucleus but, rather, a smaller effective charge, owing to the partial screening of the nuclear charge by the charge density cloud created by the second electron. To find this effective charge Zeff, we use a variational method (studied in detail later, in Chapter 41). Namely, we consider a modified wave function, with Z Zeff, so that Z effe-Z(+2)/40 and evaluate the Hamiltonian in this effective state, E= + 2m 2m But we saw in Chapter 18 that (21.34) Ze (21.35) + Z 1 Zeff = ao n 4's) = ao Ze 1 (21.36) eff = => 2ao n 2a0 () () 2m so that the energy functional to be minimized is Ze E=2ef -2- 2a0 ZZene 5 Zene + ao 8 a Minimizing this over Zeff at fixed Z by 8E/8Zeff = 0, we obtain 5 Zen = Z - 16' Replacing it back in (21.37), we find the correct minimized energy as E=- Z ao - 2 5 16 = ZZe ao (21.37) (21.38) (21.39)