Apply the variational method (Approximation 3) to the case in exercise 1.

Data From Exercise 1:-

Consider a helium atom with one electron in the \(n=1, l=0\) state, and another in the \(n=2, l=0\) state. Calculate the energy of the ortho-helium state (the lowest energy state for these quantum numbers), using the two approximations in the text (Approximation 1 and Approximation 2).

Data From Approximation 1 and 2:-

Approximation 1:

Approximation 2:

Data From Approximation 3:-

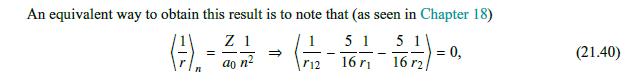
= We neglect the interaction between the electrons, 12 consider eigenfunctions of the noninteracting Hamiltonian, +, e/r12, for the wave functions, and so (21.5) and then, as in the noninteracting case, we can separate variables, obtaining eigenfunctions (F1, F2)=4(71)4(72). For these eigenfunctions, the eigenenergies are E = E(1) + E(2), (21.6) Ze 2m (21.7) and (4(1), E), ((72), E(2)) are solutions of a hydrogen-like (noninteracting) Schrdinger equation, (---.). (21.8) 4(s) (Fs) = E()) (Fs). Then the individual electron wave functions are (s) (Fs) = n,l,m, (Fs) = 4q, (Fs), (21.9) and their energies are mZ 1 Z 1 E(s) = Ens (21.10) 2h2 n 2ao n The corresponding symmetric (spin singlet) and antisymmetric (spin triplet) coordinate wave functions are (1,2)=14 (71) 42 (72) + 4qz (F1)q (F2)] - Da(1,72) = 14 [4 (1)4(F2) 4921) 49 (F2)]. (21.11)