Use the solution given in Problem 20 to rewrite the solution of Example 1 in an alternative integral form. Then use the change of variables v = 7)/2vra and the results of Problem 11 in Exercises 14.1 to show that the solution of Example 1 can be expressed as

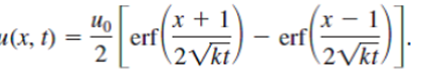
(reference problem 20)

In Problem use the Fourier integral transforms of this to solve the given boundary-value problem. Make assumptions about boundedness where necessary.

If

then the convolution theorem for the Fourier transform is given by

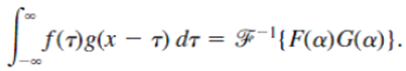
Use this result and

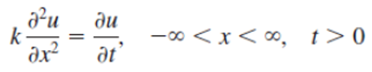
Show that a solution of the boundary-value problem

(reference example 2)

Example 2 Using the Cosine Transform

The steady-state temperature in a semi-infinite plate is determined from

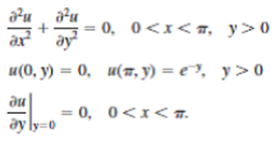
Solve for u (x, y).

(Reference problem 11 of section 14.1)

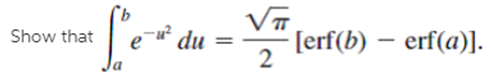
u(x, t) 120 [err ( x + 1 2kt erf (x-1 2kt 1)]. F{f(x)} = F(a) and F{g(x)} = G(a), f. f(7)g(x 7) dr = F{F(a)G(a)}. F{e-x14p} = 2mpe-pa to k u 2 at -00 < x < , t> 0 0, u(x, 0) = f(x), -0 is u(x, t) 1 2kmt. LJ f(T)e-(x-7)14kt dr. = 0, 0 0 ay ly=0 = 0, 0 VT Le du = (c 2 Show that [erf(b) - erf(a)].