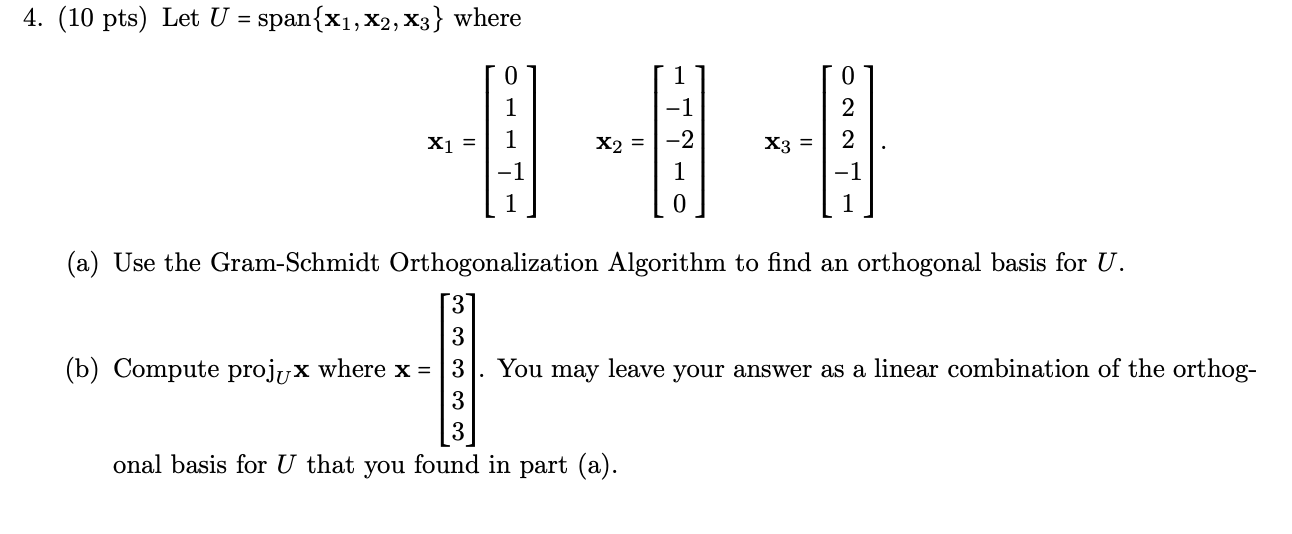
1. (15 pts) Let T : P3 - M22 be a linear transformation defined as T(p(x)) = P(0) p(1) 0 p'(0) for any p(x) EP3 where p' (x) is the derivative of the polynomial. (a) Compute the following 1. T(1 + 2x + 3x2 + 4x3) 2. Find all possible p(x) = do + alt + a2x2 + a3x3 such that T(p(x)) = } }. (b) Find ker(T) and im(T). (c) Is T one-to-one? Is Tonto? Justify your answers.2. (10 pts) Consider the following subspace U = {A E Mnn | PAP is diagonal} where P E Mnn is a fixed, invertible matrix. (a) Let P = 2 3 Find a basis for U. (Hint: you may want to do part (b) first. ) (b) For a general invertible P E Mnn, find a basis for U using the following process: 1. Let V C Mnn be the set of diagonal matrices and show that T : U - V is an isomorphism where T(A) = P-1AP 2. Find a basis { D1, D2, ..., Dk} for V (you have to figure out what k should be as well). 3. Map the basis for V back to a basis for U by applying T-.3. (15 pts) Consider the following five points: (21, y1) = (-3,0) (22, 92) = (-1,0) (23, 93) = (0, 1) (24, 94) = (2,4) (25, 35) = (3, 7) (a) Setup and solve the least squares problem to find the best fit line. Please write your answer as using fractions, not decimals. (b) Setup, but do not solve the least squares problem to find the best fit quadratic. (c) Setup, but do not solve the least squares problem to find the best fit model of the form y = aex - 1 where e is the natural number. If necessary, leave your setup in terms of e.4. (10 pts) Let U = span {X1, X2, x3} where O -1 INNO X1 = 1 X2 = X3 = -1 OHN (a) Use the Gram-Schmidt Orthogonalization Algorithm to find an orthogonal basis for U. (b) Compute projux where x = You may leave your answer as a linear combination of the orthog- onal basis for U that you found in part (a)