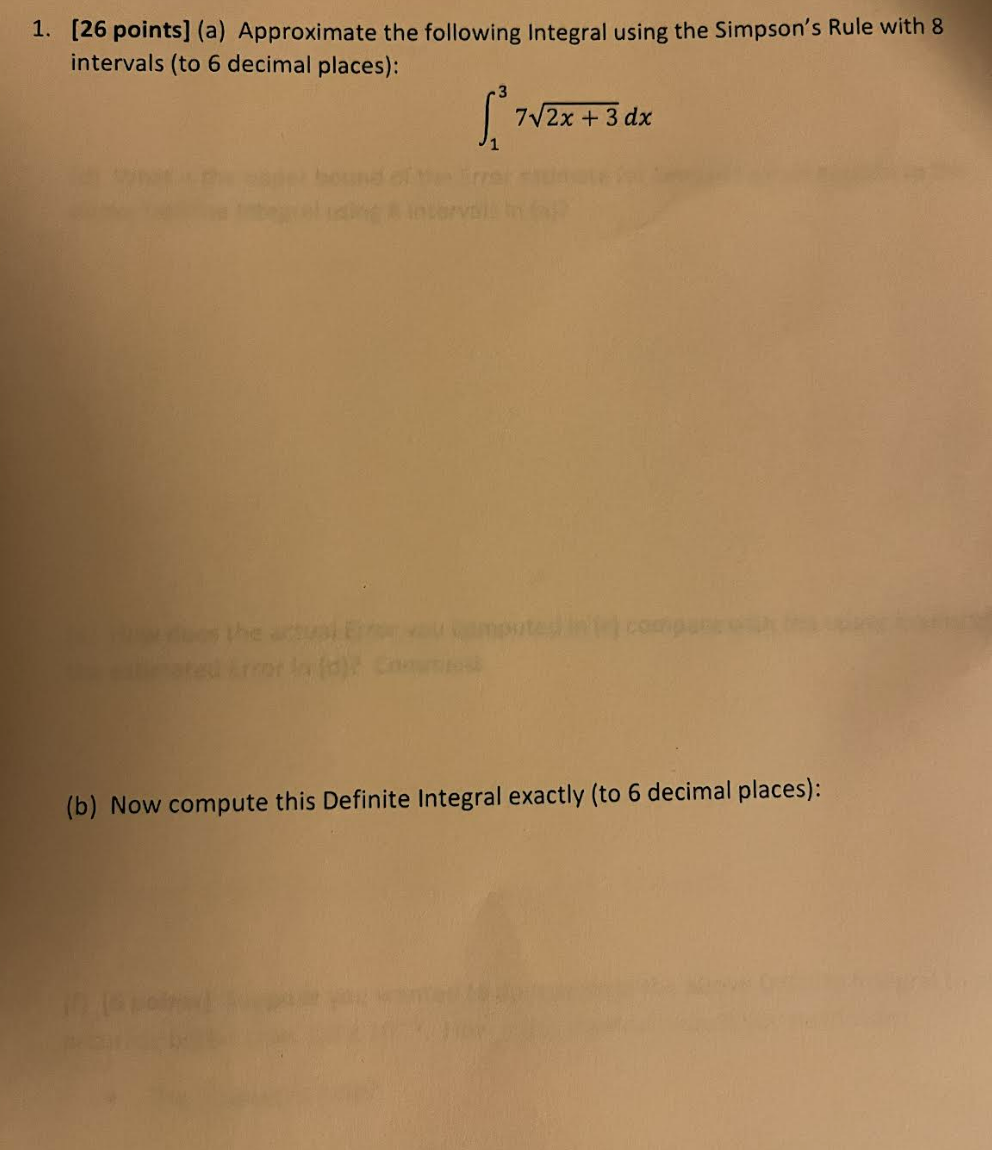
1. [26 points] (a) Approximate the following Integral using the Simpson's Rule with 8 intervals (to 6 decimal places): 7V2x + 3 dx (b) Now compute this Definite Integral exactly (to 6 decimal places):(c) What is the Absolute Error between the approximate and exact values of the Definite Integral? (d) What is the upper bound of the Error estimate for Simpson's Rule applied to the above Definite Integral using 8 intervals in (a)? (e) How does the actual Error you computed in (c) compare with the upper bound of the estimated Error in (d)? Comment. (f) [6 points] Suppose you wanted to approximate the above Definite Integral to an accuracy better than 1.0 x 10-6. How many intervals would you need with: . The Simpson's Rule?. The Trapezoidal Rule? . The Mid Point Rule? Compare and comment on the number of intervals needed by each approximate Integration Rule (above)