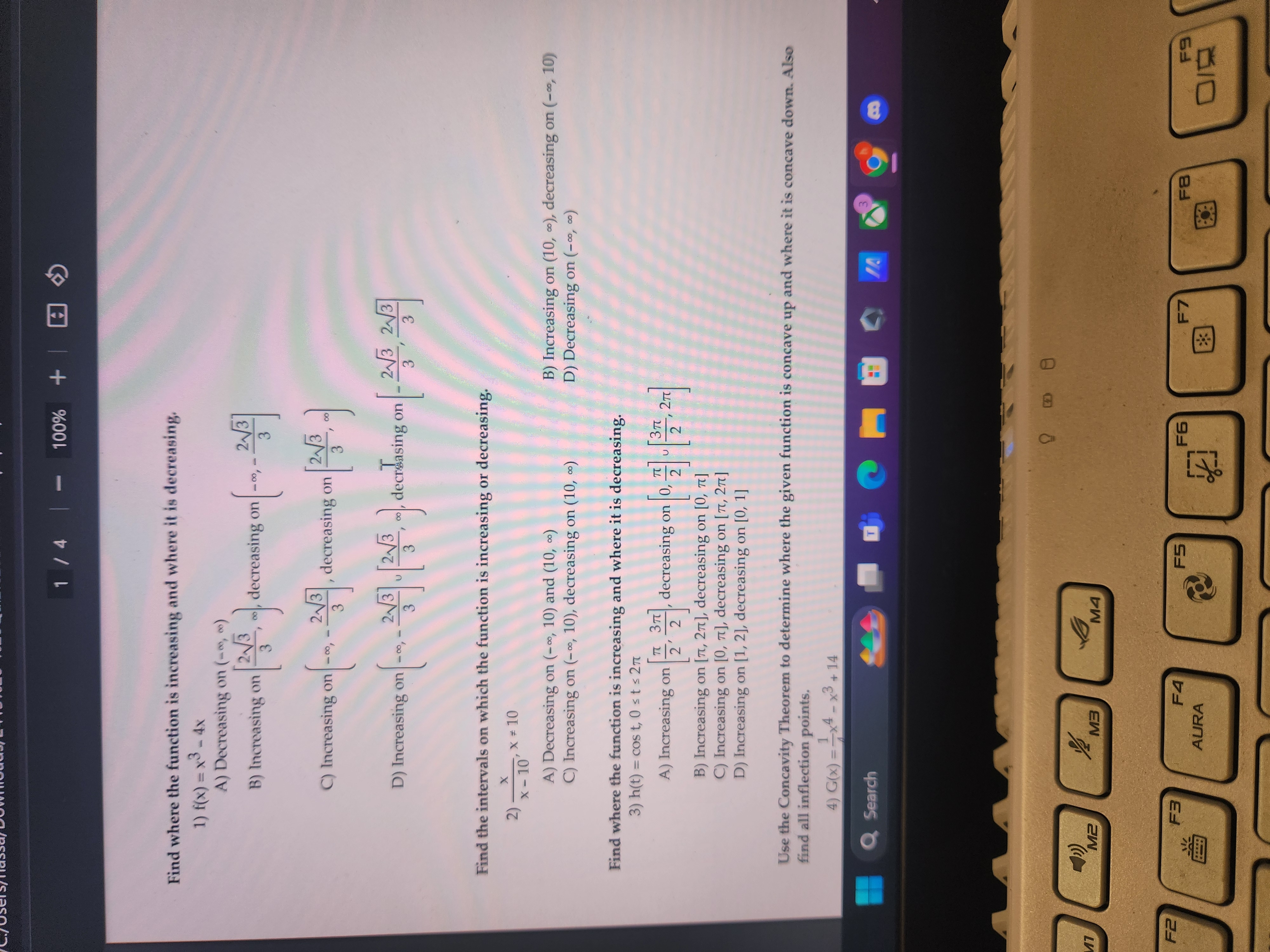
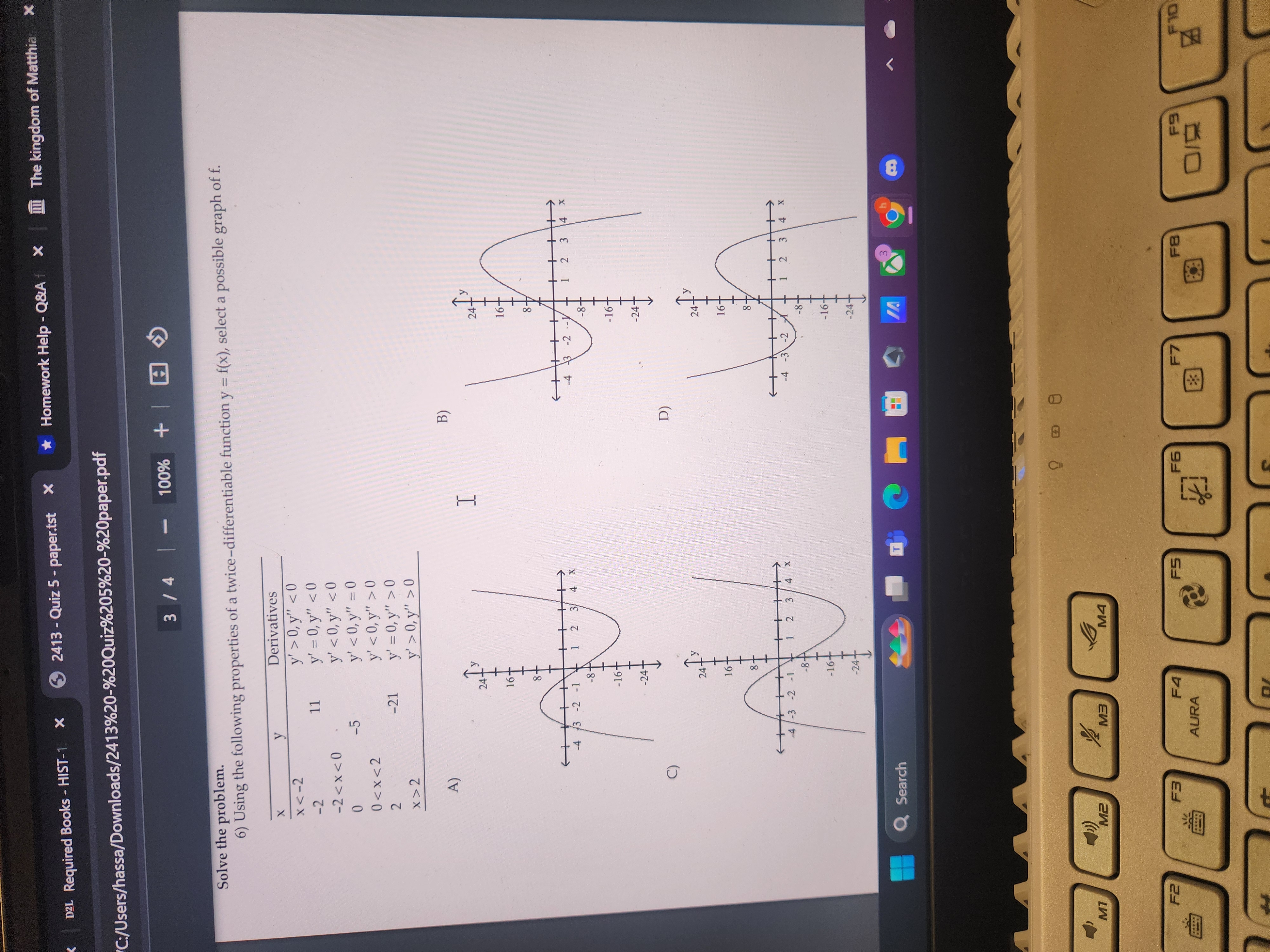
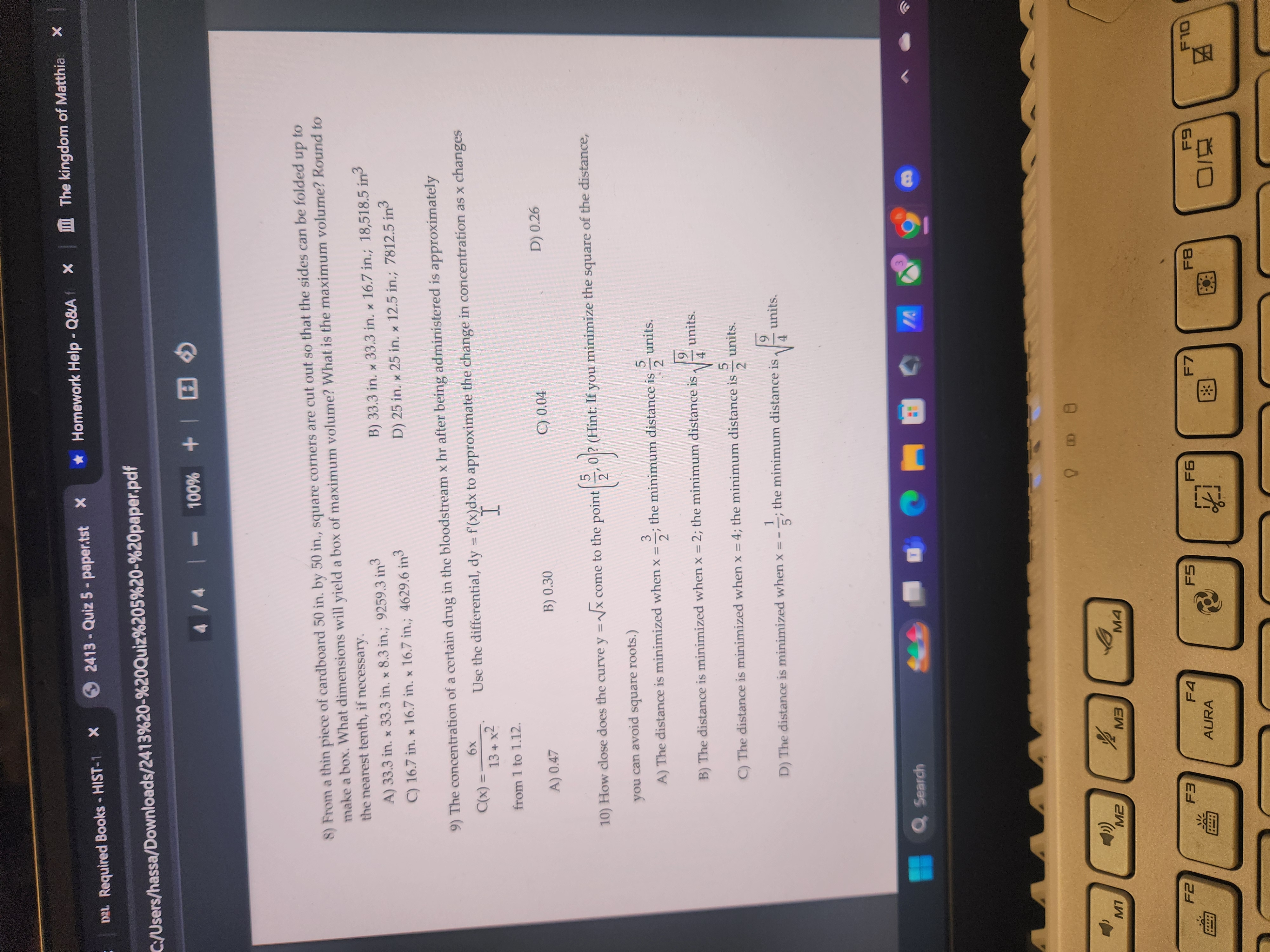
1 /4 100% + Find where the function is increasing and where it is decreasing. 1) f(x) = x3 - 4X A) Decreasing on (-60, 6) B) Increasing on 213, .., decreasing on -co, - 21/3 C) Increasing on -0, - 21/3 , decreasing on 21/3, D) Increasing on -0., - -u , . . decreasing on - 21/3, 213 Find the intervals on which the function is increasing or decreasing. 2 ) - x - 10' X # 10 A) Decreasing on (-0, 10) and (10, 0.) B) Increasing on (10, co), decreasing on (-co, 10) C) Increasing on (-0, 10), decreasing on (10, 0.) D) Decreasing on (-co, co) Find where the function is increasing and where it is decreasing. 3) h(t) = cost, 0 st s 2n A) Increasing on- 2 2 7 371, decreasing on 0, 2 2. 27 B) Increasing on [7t, 27], decreasing on [0, 7] C) Increasing on [0, 7], decreasing on [7t, 27t] D) Increasing on [1, 2], decreasing on [0, 1] Use the Concavity Theorem to determine where the given function is concave up and where it is concave down. Also find all inflection points. 4) G(x) =-x4 -x3+14 Q Search M2 MA F2 FE F4 F5 FE F7 F8 AURA FeD2L Required Books - HIST-1 X 5 2413 - Quiz 5 - paper.tst X *Homework Help - Q&A f X III The kingdom of Matthia X C:/Users/hassa/Downloads/2413%20-%20Quiz%205%20-%20paper.pdf 3 / 4 |- 100% + Solve the problem. 6) Using the following properties of a twice-differentiable function y = f(x), select a possible graph of f. X Derivatives X 0, y" 0 2 -21 y' = 0 , y" > 0 x > 2 y' > 0, y" > 0 A) B) I C) D) -4-3-2 -1 2 3 / 4 - 167 - 24+ Q Search M1 M2 M3 MA F2 F3 F4 FS AURA FE F8 F 10D21. Required Books - HIST-1 X 2413 - Quiz 5 - paper.tst X *Homework Help - Q&Af X III The kingdom of Matthia X C:/Users/hassa/Downloads/2413%20-%20Quiz%205%20-%20paper.pdf 4/4 1- 100% + 8) From a thin piece of cardboard 50 in. by 50 in., square corners are cut out so that the sides can be folded up to make a box. What dimensions will yield a box of maximum volume? What is the maximum volume? Round to the nearest tenth, if necessary. A) 33.3 in. x 33.3 in. x 8.3 in.; 9259.3 in3 B) 33.3 in. x 33.3 in. x 16.7 in.; 18,518.5 in3 C) 16.7 in. x 16.7 in. x 16.7 in.; 4629.6 in3 D) 25 in. x 25 in. x 12.5 in.; 7812.5 in3 9) The concentration of a certain drug in the bloodstream x hr after being administered is approximately C (x ) = _ 6x Use the differential, dy = f(x)dx to approximate the change in concentration as x changes 13+ x2 from 1 to 1.12. A) 0.47 B) 0.30 C) 0.04 D) 0.26 10) How close does the curve y = Vx come to the point . 0 ? (Hint: If you minimize the square of the distance, you can avoid square roots.) A) The distance is minimized when x = ; the minimum distance is - units. B) The distance is minimized when x = 2; the minimum distance is C) The distance is minimized when x = 4; the minimum distance is ~ units. D) The distance is minimized when x = - -; the minimum distance is a units. Q Search 9 M1 M2 M3 F2 F4 F5 AURA F6 F7 F8 8:3 F9