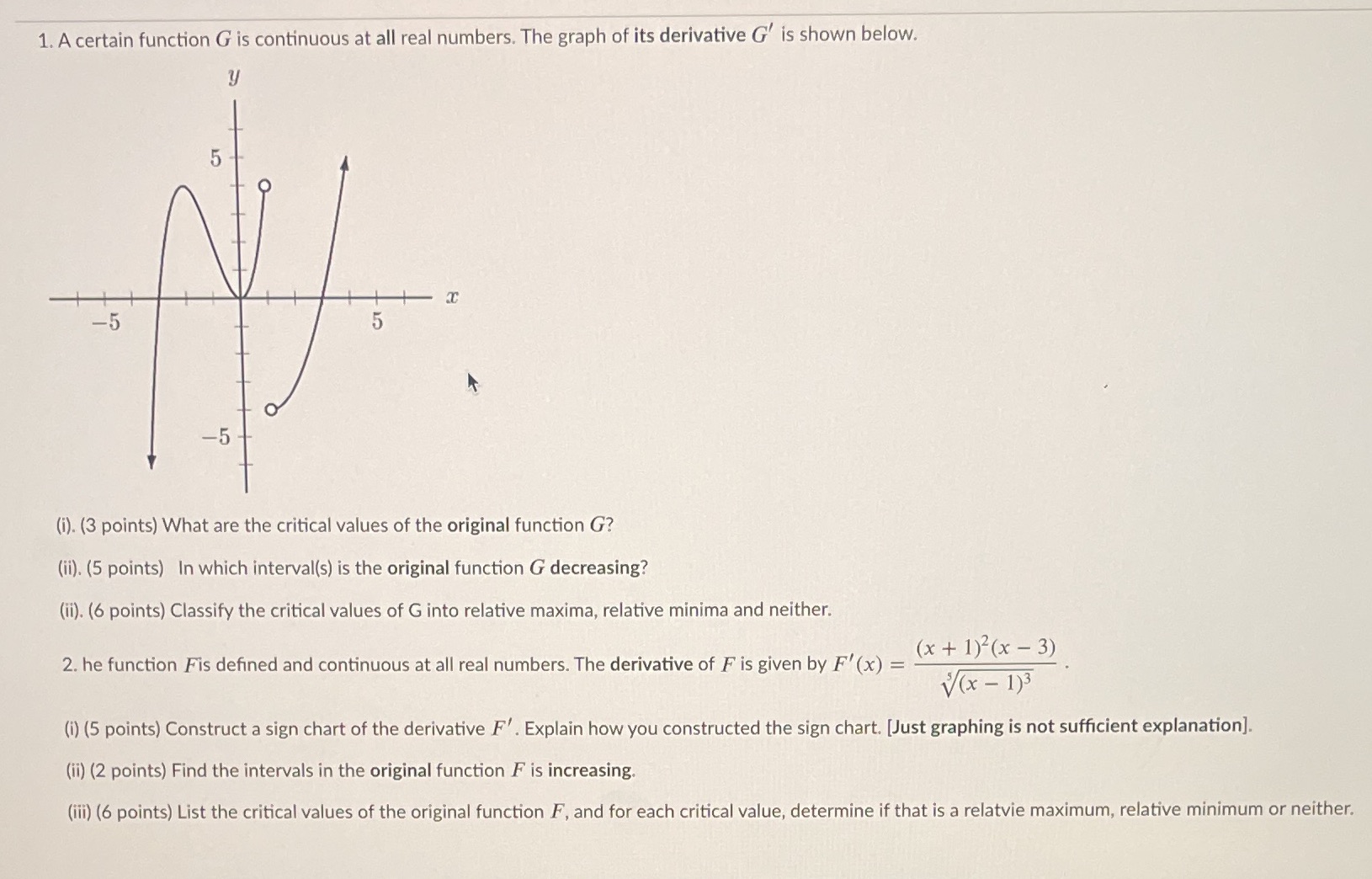
1. A certain function G is continuous at all real numbers. The graph of its derivative G' is shown below. 5 -5 5 (i). (3 points) What are the critical values of the original function G? (ii). (5 points) In which interval(s) is the original function G decreasing? (ii). (6 points) Classify the critical values of G into relative maxima, relative minima and neither. 2. he function Fis defined and continuous at all real numbers. The derivative of F is given by F' (x) = (x + 1) ( x - 3) V( x - 1)3 (i) (5 points) Construct a sign chart of the derivative F . Explain how you constructed the sign chart. [Just graphing is not sufficient explanation]. (ii) (2 points) Find the intervals in the original function F is increasing. (iii) (6 points) List the critical values of the original function F, and for each critical value, determine if that is a relatvie maximum, relative minimum or neither