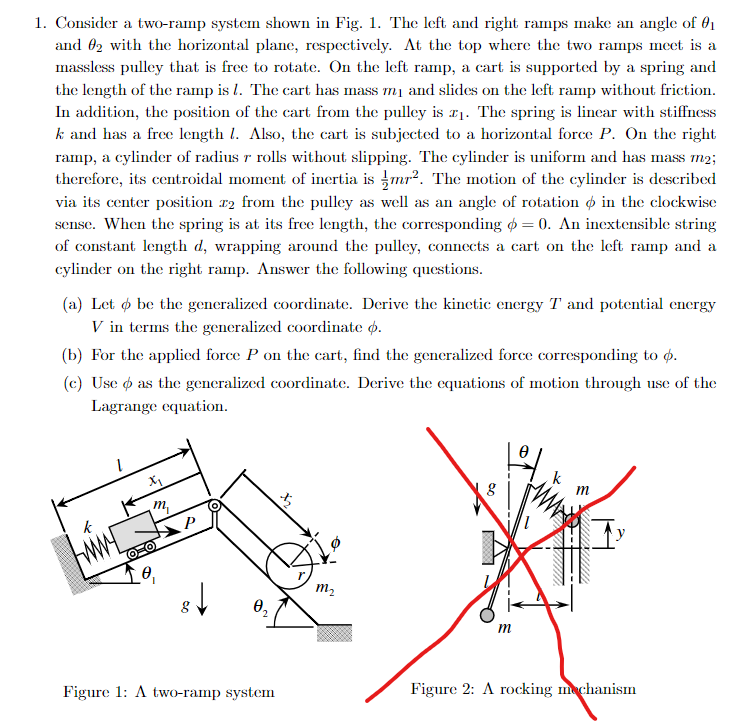
$1.$ Consider a two$-$ramp system shown in Fig. $1.$ The left and right ramps make an angle of $\backslash (\backslash$theta$\_\{1\}\backslash )$ and $\backslash (\backslash$theta$\_\{2\}\backslash )$ with the horizontal plane, respectively. At the top where the two ramps meet is a massless pulley that is free to rotate. On the left ramp, a cart is supported by a spring and the length of the ramp is $\backslash ($ l $\backslash ).$ The cart has mass $\backslash ($ m$\_\{1\}\backslash )$ and slides on the left ramp without friction. In addition, the position of the cart from the pulley is $\backslash ($ x$\_\{1\}\backslash ).$ The spring is linear with stiffness $\backslash ($ k $\backslash )$ and has a free length $\backslash ($ l $\backslash ).$ Also, the cart is subjected to a horizontal force $\backslash ($ P $\backslash ).$ On the right ramp, a cylinder of radius $\backslash ($ r $\backslash )$ rolls without slipping. The cylinder is uniform and has mass $\backslash ($ m$\_\{2\}\backslash )$; therefore, its centroidal moment of inertia is $\backslash (\backslash$frac$\{1\}\{2\}$ m r$^\{2\}\backslash ).$ The motion of the cylinder is described via its center position $\backslash ($ x$\_\{2\}\backslash )$ from the pulley as well as an angle of rotation $\backslash (\backslash$phi $\backslash )$ in the clockwise sense. When the spring is at its free length, the corresponding $\backslash (\backslash$phi$=0\backslash ).$ An inextensible string of constant length $\backslash ($ d $\backslash ),$ wrapping around the pulley, connects a cart on the left ramp and a cylinder on the right ramp. Answer the following questions.

$($a$)$ Let $\backslash (\backslash$phi $\backslash )$ be the generalized coordinate. Derive the kinetic energy $\backslash ($ T $\backslash )$ and potential energy $\backslash ($ V $\backslash )$ in terms the generalized coordinate $\backslash (\backslash$phi $\backslash ).$

$($b$)$ For the applied force $\backslash ($ P $\backslash )$ on the cart, find the generalized force corresponding to $\backslash (\backslash$phi $\backslash ).$

$($c$)$ Use $\backslash (\backslash$phi $\backslash )$ as the generalized coordinate. Derive the equations of motion through use of the Lagrange equation.

Figure $1$: $\backslash (\backslash$Lambda $\backslash )$ two$-$ramp system