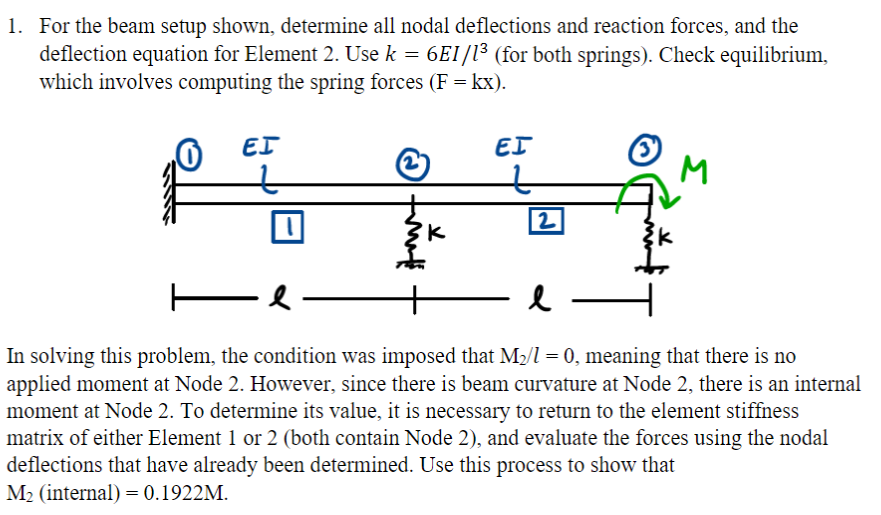
$1.$ For the beam setup shown, determine all nodal deflections and reaction forces, and the deflection equation for Element $2.$ Use $\backslash ($ k$=6$ E I $/$ l$^\{3\}\backslash )($for both springs$).$ Check equilibrium, which involves computing the spring forces $\backslash ((\backslash$mathrm$\{$F$\}=\backslash$mathrm$\{$kx$\})\backslash ).$

In solving this problem, the condition was imposed that $\backslash (\backslash$mathrm$\{$M$\}\_\{2\}/$ l$=0\backslash ),$ meaning that there is no applied moment at Node $2.$ However, since there is beam curvature at Node $2,$ there is an internal moment at Node $2.$ To determine its value, it is necessary to return to the element stiffness matrix of either Element $1$ or $2($both contain Node $2),$ and evaluate the forces using the nodal deflections that have already been determined. Use this process to show that $\backslash (\backslash$mathrm$\{$M$\}\_\{2\}(\backslash )$ internal $\backslash ()=0\mathrm{.}1922\backslash$mathrm$\{$M$\}\backslash ).$