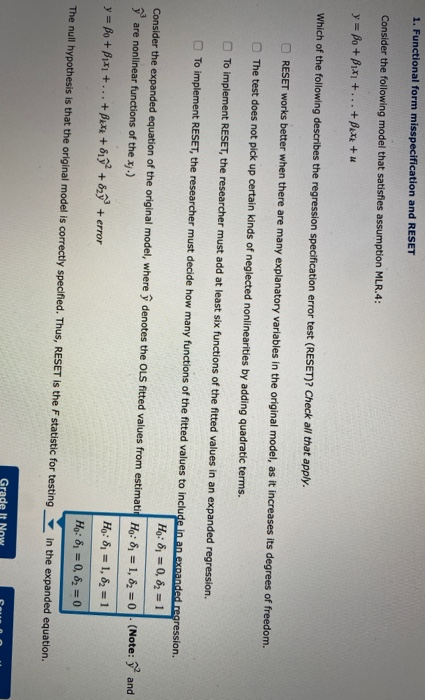
Question: 1. Functional form misspecification and RESET Consider the following model that satisfies assumption MLR.4: y = Bo + Bixi + ... + x + u
1. Functional form misspecification and RESET Consider the following model that satisfies assumption MLR.4: y = Bo + Bixi + ... + x + u Which of the following describes the regression specification error test (RESET)? Check all that apply. RESET works better when there are many explanatory variables in the original model, as it increases its degrees of freedom. The test does not pick up certain kinds of neglected nonlinearities by adding quadratic terms. To implement RESET, the researcher must add at least six functions of the fitted values in an expanded regression. To implement RESET, the researcher must decide how many functions of the fitted values to include in an expanded regression. H: 8; = 0,8 = 1 Consider the expanded equation of the original model, where denotes the OLS fitted values from estimatin Ho: 81 = 1, 82 = 0 (Note: y and are nonlinear functions of the xj.) H: 8 = 1,83 = 1 y = Bo + B +...+Bext + 8192 + 829 + error H: 8 = 0,8 = 0 The null hypothesis is that the original model is correctly specified. Thus, RESET is the F statistic for testing In the expanded equation. 2. Tests against nonnested alternatives Suppose you are trying to decide whether an independent variable should appear in level (nonnested Model 1) or logarithmic (nonnested Model 2 form. Since these are nonnested models, we cannot use a standard F test to test for joint significance. Model 1 y = Bo + B1X1 + B2x2 + x Model 2 y = Bo + Bilog(xi) + Balog(x2) + u True or False: One way to test Model 1 against Model 2, to determine the form in which the independent variable should appear, is by estimating Model 1 by OLS and using the fitted values, 9, from this as another regressor in the original Model 2. From here, the Davidson-MacKinnon test is obtained from the t statistic on the fitted values, , in the auxiliary equation: y = Bo + Bilog(x1) + Bzlog(x2)++ error. (Hint: Assume that Model 1 holds with E/ulx, 12) = 0.) True False Which of the following describe(s) potential issues with nonnested testing? Check all that apply. The nonnested testing works best in cases when the models have different dependent variables. The nonnested testing does not apply to cases when the models have different dependent variables. Both models could be rejected, or neither model could be rejected. Rejecting Model 2 implies that Model 1 is the correct model