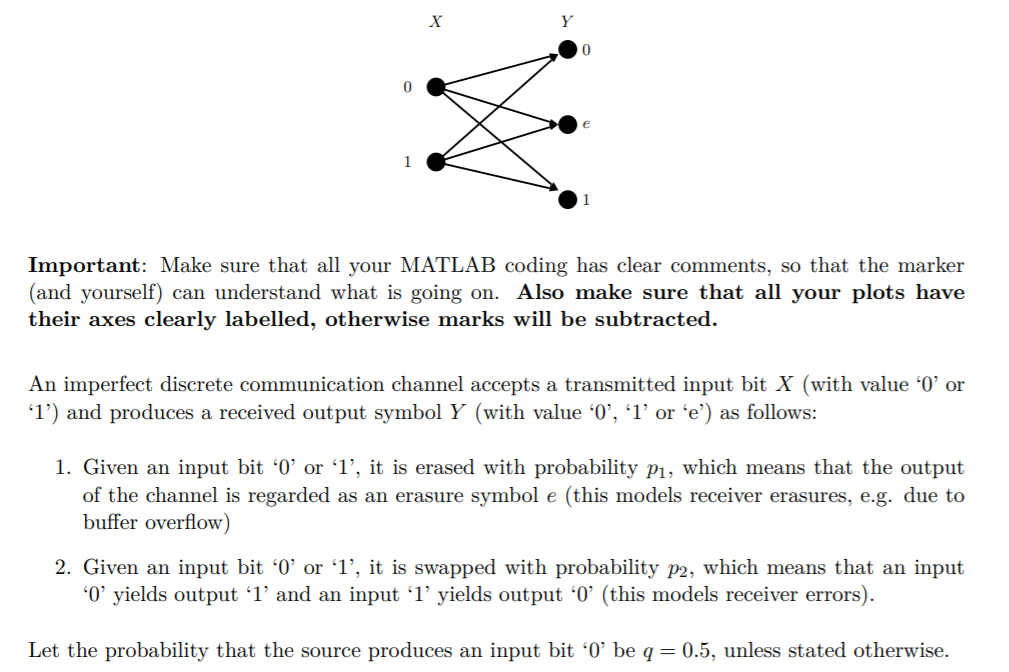
.1 Important: Make sure that all your MATLAB coding has clear comments, so that the marker (and yourself) can understand what is going on. Also make sure that all your plots have their axes clearly labelled, otherwise marks will be subtracted. An imperfect discrete communication channel accepts a transmitted input bit X (with value '0' or '1') and produces a received output symbol Y (with value '0', '1' or 'e') as follows: 1. Given an input bit '0' or '1', it is erased with probability 331, which means that the output of the channel is regarded as an erasure symbol e (this models receiver erasures, e.g. due to buer overow) 2. Given an input bit '0' or '1', it is swapped with probability p2, which means that an input '0' yields output '1' and an input '1' yields output '0' (this models receiver errors). Let the probability that the source produces an input bit '0' be q = 0.5, unless stated otherwise. d) (5 marks) Assume that p1 = 0 and p2 = 0.05. Suppose we try and communicate the value X of one input bit via n = 99 independent uses of this channel via repetition coding. In other words, thinking of each channel use as a separate time-slot, we transmit the value of the input bit \"n, times. Thus we transmit either the bit string 00. . .0 or the bit string 11. .. 1 (these are strings of length n). Let Sn be the number of occurring bit-swaps. Taking n = 99, rst nd an exact expression for its pmi1 then nd a Poisson approximation for this expression. Plot both the exact and the approximate pmf (use your Poisson expression), using MATLAB; compare and comment. g) (5 marks) Assume that n is any positive odd integer > 1, p1 = 0 and that p2 has a value