Question: 1. Let f(n) = 2n + 1, n = 0, 1, 2.... Define f(n) recursively. 2. Let f(n) = n^2 , n = 1, 2....

1. Let f(n) = 2n + 1, n = 0, 1, 2.... Define f(n) recursively.

2. Let f(n) = n^2 , n = 1, 2.... Define f(n) recursively.

3. Prove that 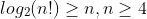1. Let f(n) = 2n + 1, n = 0, 1, 2.....

4. Determine whether each of the following is a one-to-one and/or an onto. Give a proof or provide a counterexample to justify your answer.

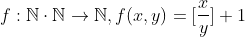
Define f(n) recursively. 2. Let f(n) = n^2 , n = 1,

logz(n!) > n, n > 4

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Q:

Indicate whether each phrase is more descriptive of financial accounting or managerial accounting. (a) May be subjective Financial accounting Managerial accounting (b) Often used to obtain financing...

Q:

Indicate whether each phrase is more descriptive of financial accounting or managerial accounting. (a) May be subjective Financial accounting Managerial accounting (b) Often used to obtain financing...

Q:

1. Let f (n) and g(n) be asymptotically nonnegative functions. Using the basic definition of notation, prove that max (fin), g(n)) = (f(n) + g(n)) 2. Prove that o(g(n)) n a(g(n) is the empty set.....

Q:

Indicate whether each phrase is more descriptive of financial accounting or managerial accounting. (a) May be subjective Financial accounting Managerial accounting (b) Often used to obtain financing...

Q:

(1) Let f : [n] r [n] be a permutation. Axed point of f is an element x E [n] such that f(x) = x. Now consider random permutations of [n] and let X be the random variable which represents the number...

Q:

(1) Let f : [n] r [n] be a permutation. Axed point of f is an element x E [n] such that f(x) = x. Now consider random permutations of [n] and let X be the random variable which represents the number...

Q:

Question 5 1 pts We want to prove that n +(m - n) = m for all n, m N= {0, 1, 2,...}. We rearrange the terms to n - n + m and cancel out both ns to get m The proof is correct. The proof is essentially...

Q:

When developing financial statement forecasts, analysts should most likely: a) Develop possibilities relying exclusively on the results of financial analysis b) Use the results of financial analysis,...

Q:

Computer Science, Algorithm Design and Analysis 1. Implement a merge sort algorithm in your favorite programming language (e.g. C, Java, Python, etc.). Modify the code, so that it prints the...

Q:

MAT 137Y: Calculus! Problem Set 7. Due in tutorial on July 27/28 Instructions: Print this cover page, fill it out entirely, sign at the bottom, and STAPLE it to the front of your problem set (You do...

Q:

All electron with initial kinetic energy 6.0eV encounters a barrier with height 11.0eV. What is the probability of tunneling if the width of the barrier is? (a) 0.80 nm and (b) 0.40 run?

Q:

The figure shows the circular flow model. During 2020, flow A was $278 billion, flow B was $158 billion, flow D was $56 billion, and flow E was $17 billion. Calculate GDP and government expenditure....

Q:

Your friend Jordan took a finance class where he learned about the risk - return trade - off. Eager to earn high returns, he decided to invest in a risky start - up technology company. A year later,...

Q:

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

Q:

Were the team members dependable? If not, how were they held accountable?

Q:

Which team solution is more likely to be pursued and why?

Q:

1. I can read fellow team members true feelings, even if they try to hide them.