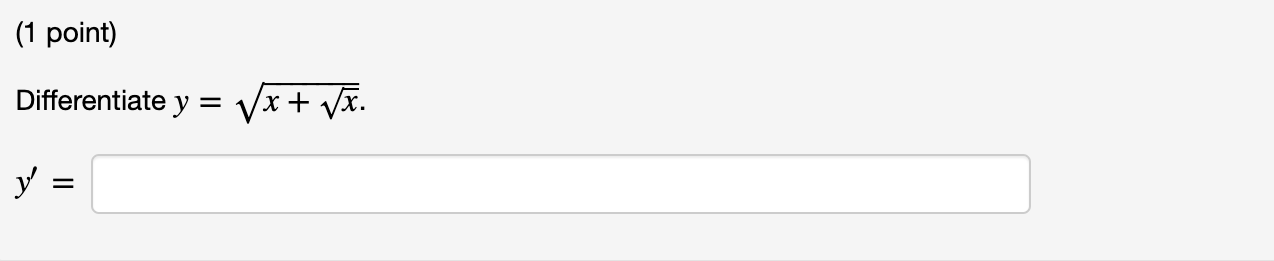
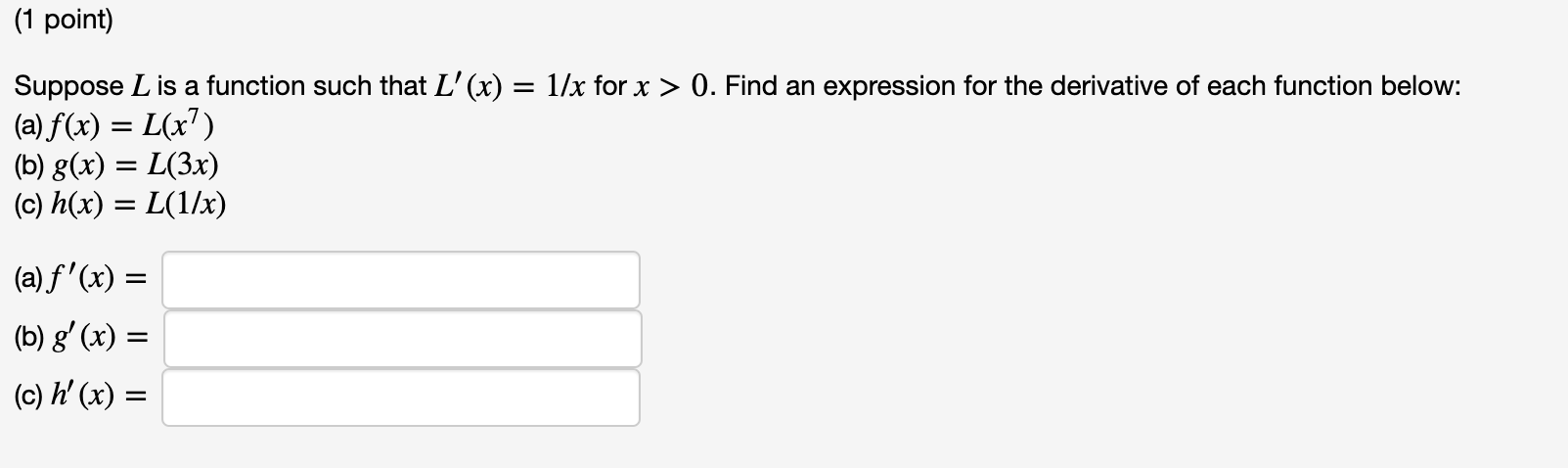
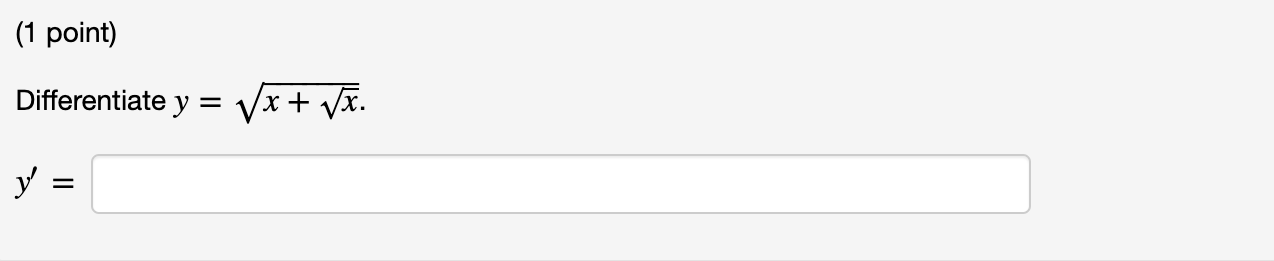
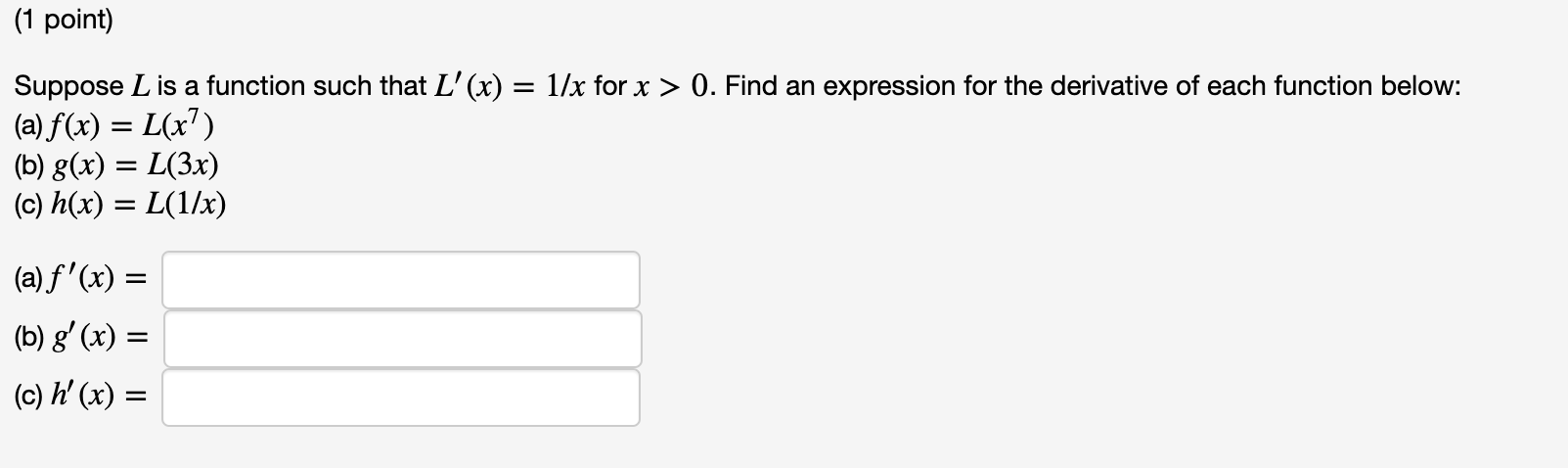
(1 point) Differentiate y = 107-x2 y =(1 point) Differentiate y = -8 cot2 (sin t).\f(1 point) Suppose L is a function such that L' (x) = llx for x > 0. Find an expression for the derivative of each function below: (a)f(x) = L(x7) (b) 800 = L(3x) (c) h(x) = L(1/x) (a)f '(x) = (b) g' (X) = (C) h' (x) = \f(1 point) By writing Ixl = vx2 and using the Chain Rule, one can verify that a Ixl = dx (a) If f(x) = I sin xl, find f' (x). (b) Where is f(x) not differentiable? Merely give the smallest positive value of x. (c) If g(x) = sin Ixl, find g' (x). (d) Where is g(x) not differentiable? (a) f'(x) = (b) At x = (c) g' (x) = (d) At x =