Question: (1 point) Find a basis {p(x), q(x)} for the kernel of the linear transformation L : P3 [x] R defined by L(f(x)) = f'(-7)

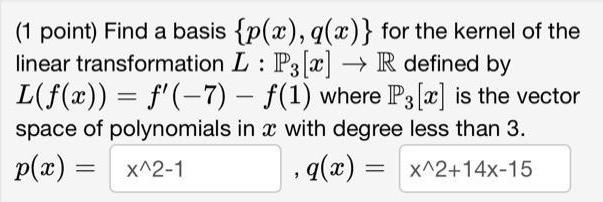
(1 point) Find a basis {p(x), q(x)} for the kernel of the linear transformation L : P3 [x] R defined by L(f(x)) = f'(-7) - f(1) where P3 [x] is the vector space of polynomials in a with degree less than 3. p(x) = x^2-1 q(x) = x^2+14x-15

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Table 1 Forecast Forecast Forecast Forecast Forecast 12/31/2021 12/31/2022 12/31/2023 12/31/2024 12/31/2025 12/31/2026 Actual Fiscal Year End Income Statement Sales (Net) Cost of goods sold 20,000...

Hi Erylee88, I would like to utilize your service again. Same format different questions. Please find attached document for your review. Let me know. Thank you, Sam...

4. Let P\" be the vector space of polynomials of degree at most n. (a) Consider the linear transformation L : P3 > P2: L(p(3:)) = p'(:c) + 13(1). Find the matrix representing L with respect to the...

*****see note below with stars***** You manage Human Relations for your company. One of your sales managers has retired, leaving an opening. You are considering two different employees for the...

s sf Define the terms opaque type and concrete type. [5 marks] The following is a shortened version of one of the definition modules described in the Modula-2 user manual: Provide a suitable...

COMPLETE SLUTION IN WRITTEN FORM NO IMAGEAND ONLY ORIGINAL WORK \fAssume that f(x) = 6x + 14 and g(x) = 5x - 1. Find the composition (fog)(x) (A) 30x + 20 (B) 30x + 13 (C) 30x + 69 (D) 30x + 8 The...

Linear Algebra Final answer only - No Explanation Section 4.2 Matrix of Transformations: Problem 7 :1 point: Find the malrix A of the linear transformation T from lit\" to R2 that rotates any...

Hi There, I need someone to help me with the attached finance worksheet. There are 3 problems in this excel file - one problem on each individual tab. I am attaching a couple of additional files as...

Please help me find the answers to the practice question and please provide work, Exercise 7.6.4: Understanding the Fundamental Theorem of Matrix Representations. Consider the linear transformation :...

buckley (jdb4687) - Review - beshaj - (53521) This print-out should have 60 questions. Multiple-choice questions may continue on the next column or page - find all choices before answering. Find the...

Multi-base Company Limited is a diversified business group with interests in fabric and yarn manufacturing, paper and pulp, and cement. Its manufacturing units are located across the country and...

What happens to the separation distance between two people if they both walk north at the same rate from two locations on Earth's equator? And just for fun, where in the world is a step in every...

Which of the following is accurate regarding the auditor s responsibilities for proper supervision under PCAOB? a . Audit engagement team members are responsible for compliance with PCAOB standards...

A hula hoop and solid disc of equal radii are rolled, from rest and without slipping, down an incline plane. Which one will reach the bottom of the inclined plane first? Explain.

Product profitability analysis Petersen Pneumatic Company makes three products. Its manufacturing plant in Petersburg has three production depart ments and three service departments. The...

Cost distortions Sweditrak Corporation manufactures two models of its exer- LO 1, 3, 4 cise equipment: regular (REG) and deluxe (DLX). Its plant has two production departments, fabrication (FAB) and...

Product profitability analysis Pharaoh Phawcetts, Inc. manufactures two mod- LO 1, 3, 4, 5, els of faucets: a regular and a deluxe model. The deluxe model, introduced just 10 two years ago, has been...