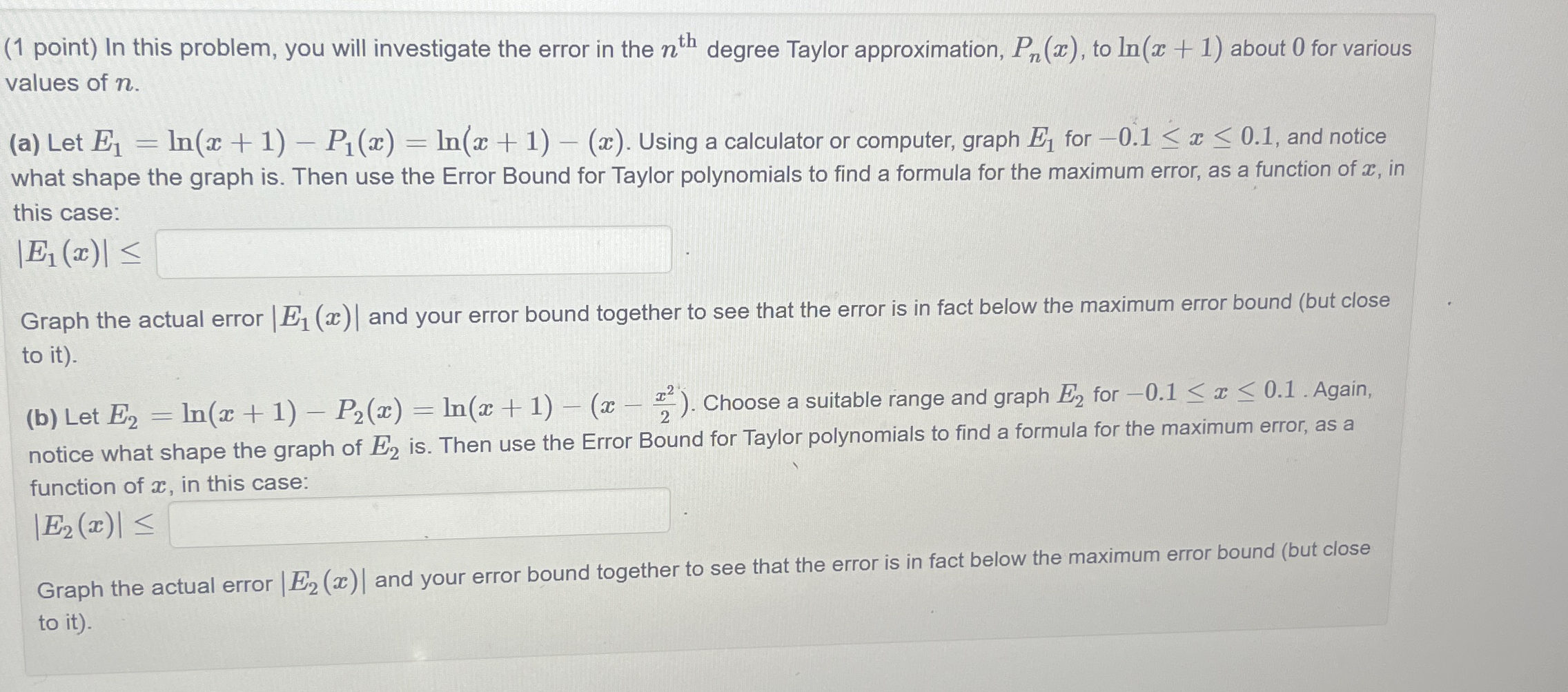
$(1$ point$)$ In this problem, you will investigate the error in the $n^{th}$ degree Taylor approximation, $P_n(x),$ to $ln(x+1)$ about $0$ for various values of $n.$

$($a$)$ Let $E_1=ln(x+1)-P_1(x)=ln(x+1)-(x).$ Using a calculator or computer, graph $E_1$ for $-0\mathrm{.}1x0\mathrm{.}1,$ and notice what shape the graph is$.$ Then use the Error Bound for Taylor polynomials to find a formula for the maximum error, as a function of $x,$ in this case:

$|E_1(x)|$

$$

Graph the actual error $|E_1(x)|$ and your error bound together to see that the error is in fact below the maximum error bound $($but close to it$).$

$($b$)$ Let $E_2=ln(x+1)-P_2(x)=ln(x+1)-(x-\frac{x^2}{2}).$ Choose a suitable range and graph $E_2$ for $-0\mathrm{.}1x0\mathrm{.}1.$ Again, notice what shape the graph of $E_2$ is$.$ Then use the Error Bound for Taylor polynomials to find a formula for the maximum error, as a function of $x$ in this case:

$|E_2(x)|$

$$

Graph the actual error $|E_2(x)|$ and your error bound together to see that the error is in fact below the maximum error bound $($but close to it$).$