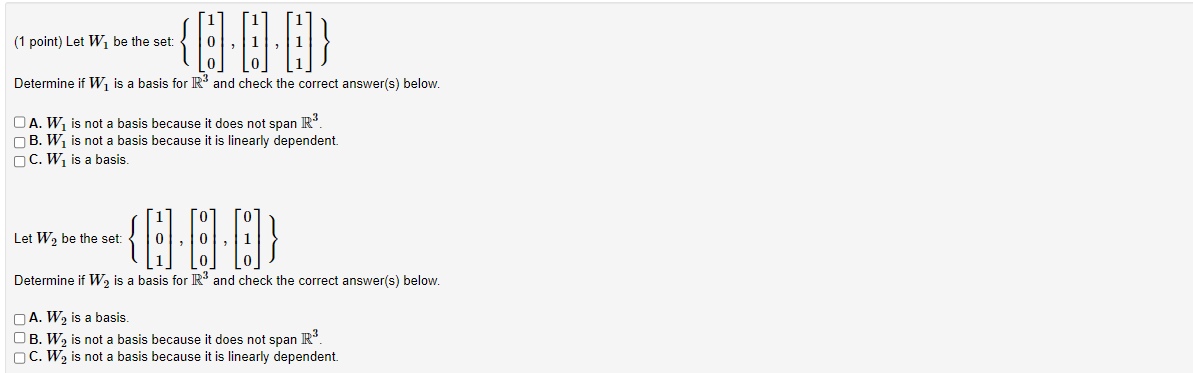
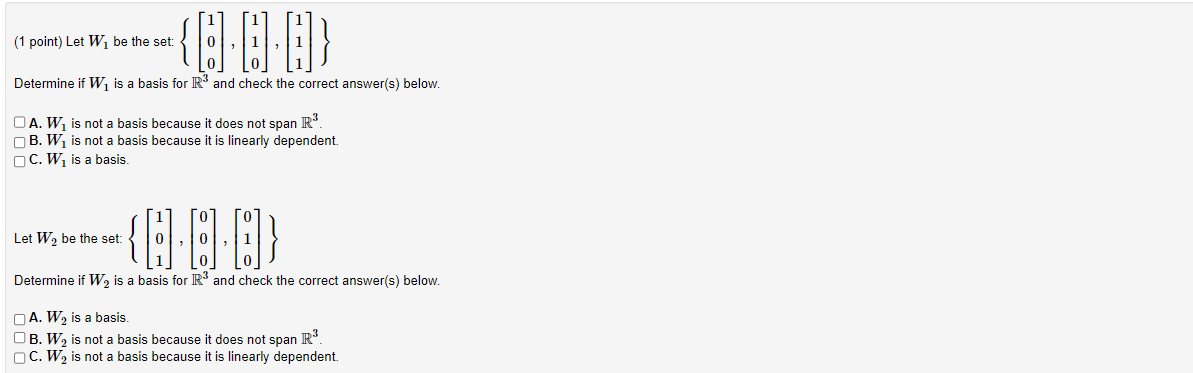
Question: (1 point) Let Wj be the set: Determine if W1 is a basis for IR and check the correct answer(s) below. O A. W, is







![the set: -3 . 9 . i] . -3 U G U](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6661187f97b5a_2956661187f85d67.jpg)
(1 point) Let Wj be the set: Determine if W1 is a basis for IR" and check the correct answer(s) below. O A. W, is not a basis because it does not span IR". B. W1 is not a basis because it is linearly dependent. O C. W1 is a basis. Let W2 be the set: Determine if W2 is a basis for IR" and check the correct answer(s) below. A. W2 is a basis. O B. W2 is not a basis because it does not span IR. C. W2 is not a basis because it is linearly dependent.('1 point) 1 -2 U {i Let W1 be the set: -3 . 9 . i] . -3 U G U 5 Determine if W1 is a basis for R3 and check the correct answeris] below. ._. A. W1 is a basis. __ B. W1 is not a basis because it is linearly dependent. D C. W1 is not a basis because it does not span R3. -2 5 Let W2 be the set: 3 . -'1 U 5 Determine if W2 is a basis for R3 and check the correct answeris] below. __ A. W2 is not a basis because it is linearly dependent. ._. B. W2 is not a basis because it does not span R3. ._. C. W2 is a basis. (1 point} Find the coordinate vector of E = 4 1 with respect to the basis B = 5 (1 point) Find a basis ofthe subspace of R4 consisting of all vectors of the form I1 711 + 1'2 221 + 933 4:1 932 Your answer should be a list of row vectors separated by commas. (Click 39.919 to learn about entering vectors.) Basis ={ }. (1 point) Find a basis of the subspace of IR* defined by the equation -4x] - 7x2 - 6x3 + 5x4 = 0. Basis
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


