Question: 1. Prove that if a real valued sequence (an) does not have an upper bound then there is a subsequence (an ) that converges to

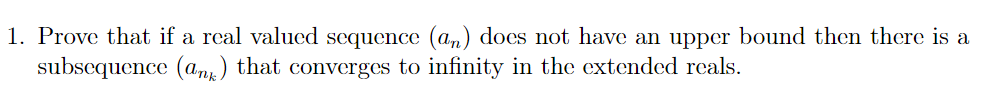
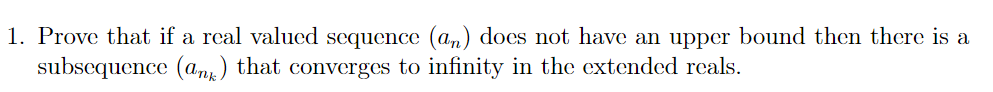
1. Prove that if a real valued sequence (an) does not

1. Prove that if a real valued sequence (an) does not have an upper bound then there is a subsequence (an ) that converges to infinity in the extended reals

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Prove that if a real valued sequence (an) does not have a lower bound then there is a subsequence (am) that converges to negative infinity in the extended reals

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

OPERATIONS MANAGEMENT ASSIGNMENT 6 1 Human resources, project management and operations management are all equally vital to a business's success. Each of these focuses on different areas of the...

Two major themes from the introduction to module 4 are "Project Management" and "Managing Risk." Discuss, in depth, your analysis of the company's actions in relation to the concepts of these two...

You$must$attach$this$cover$page$to$the$front$of$your$HW$or$you$will$lose$5$points.$ $ $ APMA$1860$Homework$2$ $ $ First$Name:$____________________________$$$Last$Name:$______________________________$...

MAT301 ASSIGNMENT 1 DUE DATE: WEDNESDAY MAY 18, 2016 AT THE BEGINNING OF YOUR TUTORIAL Question 1. Define the following relation on the integers: a b 2|(a b) Prove that this is an equivalence...

\fCPSC 121: Models of Computation Assignment #4, due Wednesday, November 18th , 2015 at 17:00 Each of the following questions asks you to prove a theorem. When the theorem is stated in English, it...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

1. What is wrong with this \"proof\"? Prove that n! > 2 n. This problem is similar to Exercise 17 in Section 6.1 of your SNHU MAT299 textbook. Assume that this is true for n = k. In other words, k! >...

Describe the steps involved in the settlement of a claim.

1. Determine the total amount of an investment of $1400 at 3.5% simple interest for 48 months. (4 marks) 2. Determine the total interest on a loan of $5000 if the interest rate is 6.24%, compounded...

Tips are the most common way occupational frauds are detected

Crisp Cookware's common stock is expected to pay a dividend of $3 a share at the end of this year (D1 = $3.00); its beta is 0.8; the risk-free rate is 5.2%; and the market risk premium is 6%. The...

Dial Digital Solutions signed a three-year lease at the beginning of the current year. The leased equipment has an economic life of five years and a fair value of $ 1,450. Under the terms of the...

You have observed the following returns over time: Assume that the risk-free rate is 6 percent and the market risk premium is 5 percent. a. What are the betas of Stocks X and Y? b. What are the...

You have observed the following returns over time: Assume that the risk-free rate is 6% and the market risk premium is 5%. a. What are the betas of Stocks X and Y? b. What are the required rates of...

Suppose that, in a hypothesis test, the null hypothesis is in fact false. a. Is it possible to make a Type I error? Explain your answer. b. Is it possible to make a Type II error? Explain your answer.

Create a 200 word summary on the Juvenile Justice System than and today. Describe The Juvenile system and provide a generalizable definition. Highlight the issues in the Juvenile system and why this...

Shellenberger Company manufactures high-end gas grills. Fixed costs amount to $19,980,000 per year. Variable costs per gas grill are $395, and the average price per gas _ | grill is $950. Required:...

Dunst and Dafoe Copy Shop (D&D) provides photocopying service. Next year, D&D estimates it will copy 2,400,000 pages at a price of $0.08 each in the coming year. Product costs include: Required:LO1...

Sharda Company is considering two different processes to make its productprocess 1 and process 2. Process 1 requires Sharda to manufacture subcomponents of the product in-house. As a result,...