$1.$ Suppose there are $1000$ users, and an attacker has a dictionary of $5000$ common passwords. An attacker has stolen the database of hashed passwords.

a$.$ If the users$$ password in the database were hashed without salt, how many Hash computation does the attacker need to find all users that have the passwords in the dictionary?

b$.$ Calculate the number of Hash computations again, now assuming salt is used for the hash.

Show you computation steps and give necessary explanations to get full credit.

$2.$In class $$authentication$,$ we explained storing Hash$10000($password$)$ as one way to $$make the guessing work expensive$.$ While doing this indeed slows down the attacker$$s offline password guessing attempt, it also significantly increases the server$$s effort. Suppose the server still stores Hash$10000($password$),$ but when Alice logs in$,$ her client machine first computes Hash$9999($password$)$ and sends that to the server.

a$.$ Will there still be the advantage gained by storing Hash$10000($password$)?$

b$.$ Will this save the server computation?

To answer both questions, first clearly give a Yes$/$No$,$ and then use a few sentences to explain why you make this conclusion.

$3.$ Consider the following authentication protocol. R is the challenge sent by Bob to Alice, and KAB is the secret Alice and Bob share. Which of the following are secure for a session key? When answering this question, for each option, think about the three aspects:

a$.$ Can Trudy impersonate Alice to Bob?

b$.$ Can this session key be securely used to encrypt messages exchanged between Alice and Bob?

c$.$ If this session key happened to be known by Trudy, can Trudy find KAB?

To get full credit, for the options that are not secure$,$ briefly explain why it is not secure$,$ you can explain by giving a case where an attacker can compromise the communication.

d$.$ KAB XOR R

e$.\{$ KAB $+$ R$\}$ KAB

f$.\{$R$\}$R$+$ KAB

g$.\{$ KAB $\}$ KAB

h$.\{$R$\}$ KAB

i$.\{$ KAB $\}$R

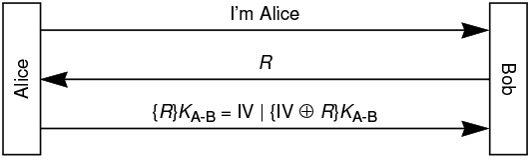
$4.$Alice and Bob use the mechanism shown in the following figure for authentication. In specific, after Alice informs Bob she wants to communicate, Bob generates a random number R and sends it back to Alice.

Assume R fits into a single block and Alice encrypts R in CBC mode, so $\{$R$\}$KAB is computed as $\{$IV xor R$\}$KAB$,$ where IV is Alice created for CBC operation. Alice then sends IV and $\{$IV xor R$\}$KAB to Bob, as shown in the $3$rd message in the figure.

Suppose Eve sees an exchange between Alice and Bob, where the challenge is R$1.$ How can Eve then impersonate Alice, during a different conversation where Bob sends a different challenge R$2?$

To get full credit, completely describe the content of messages Eve sends to Bob, and at what time. That is$,$ you need to describe the message exchange in a timeline.