1.)

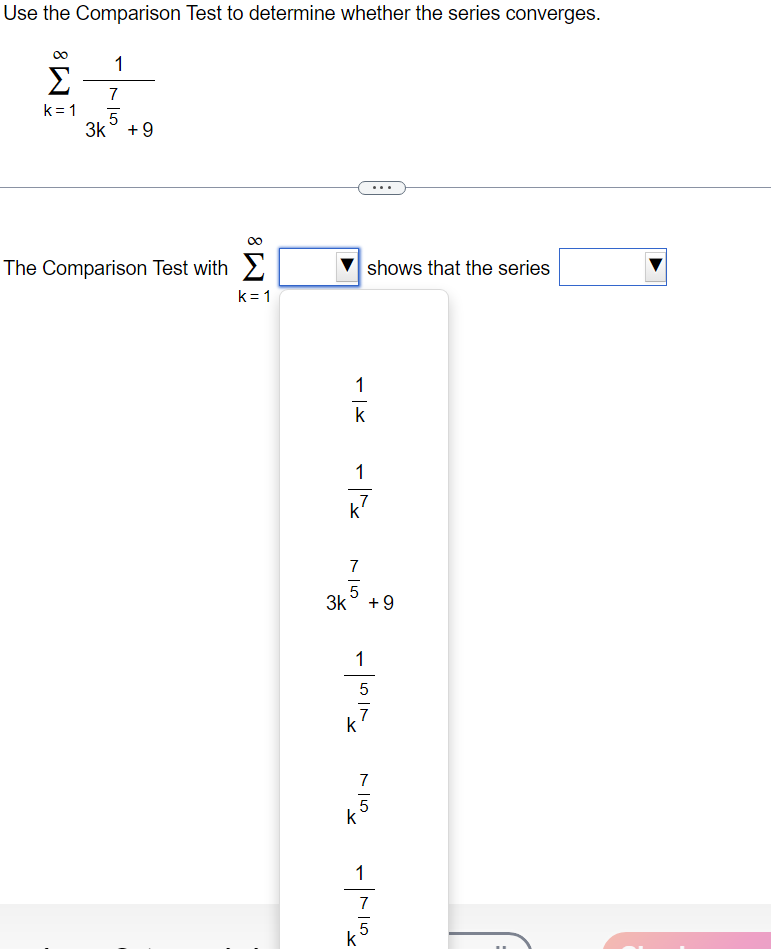
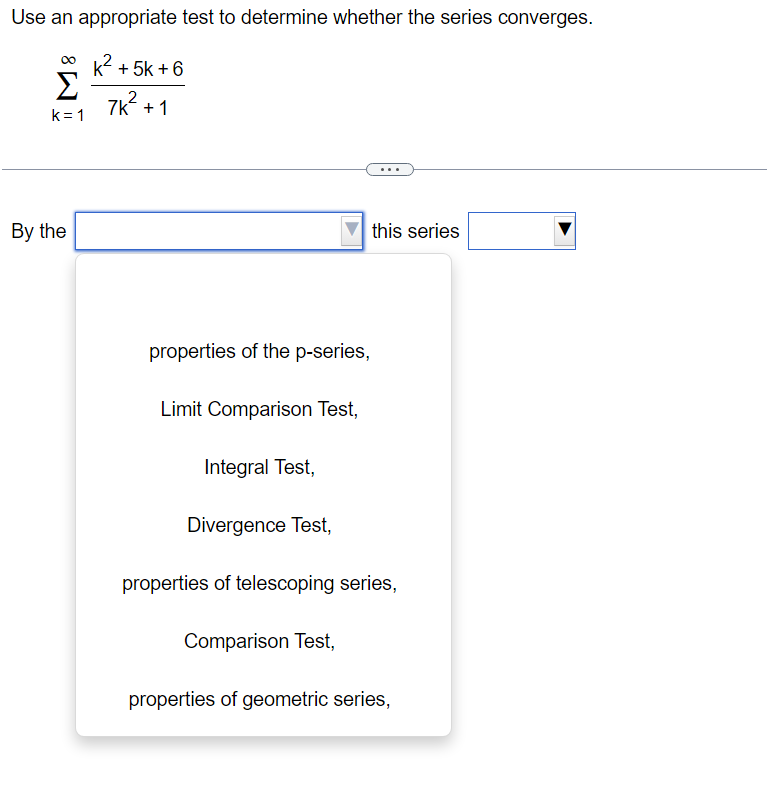
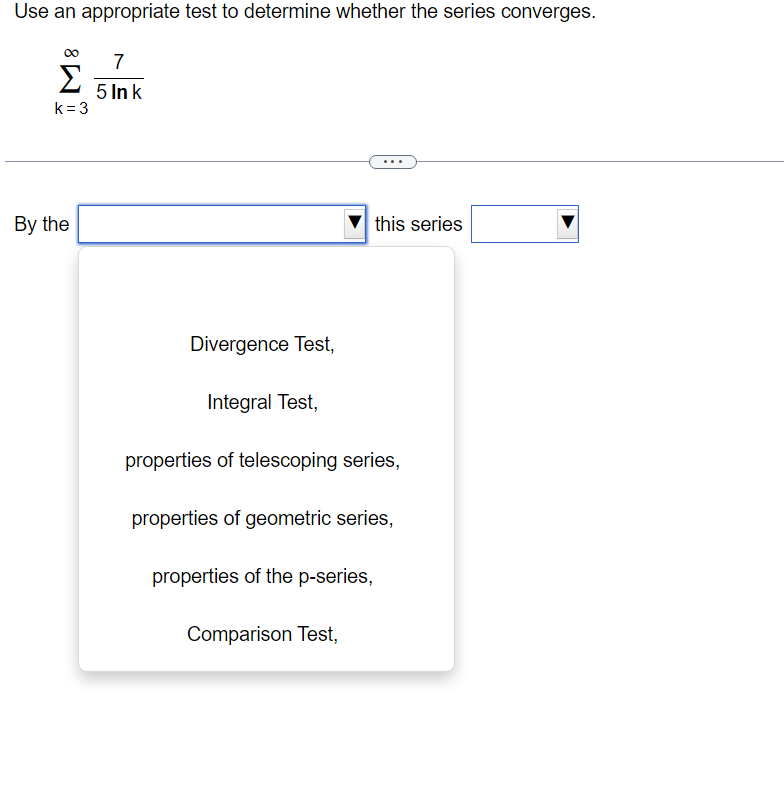
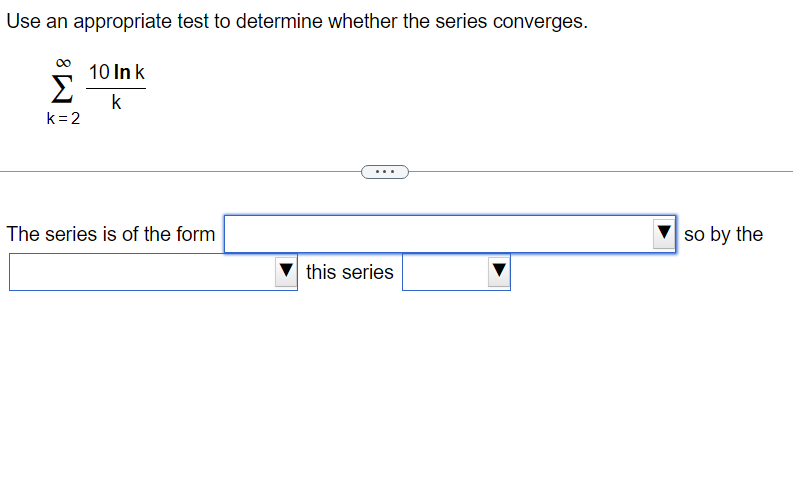
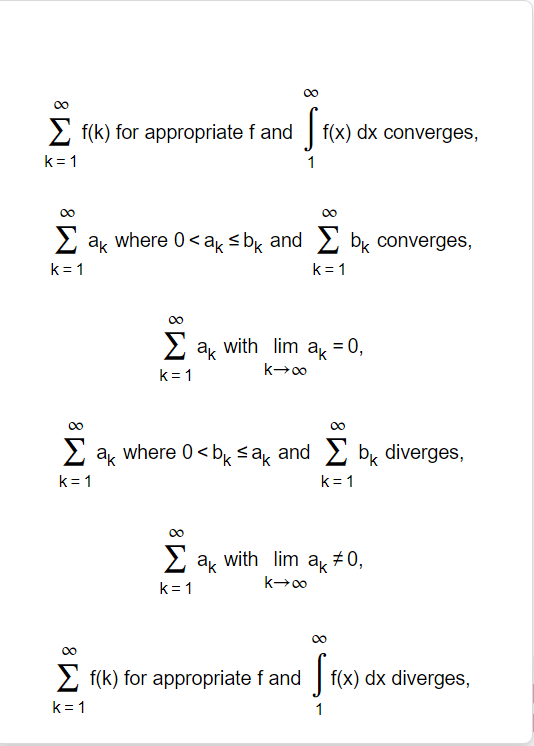
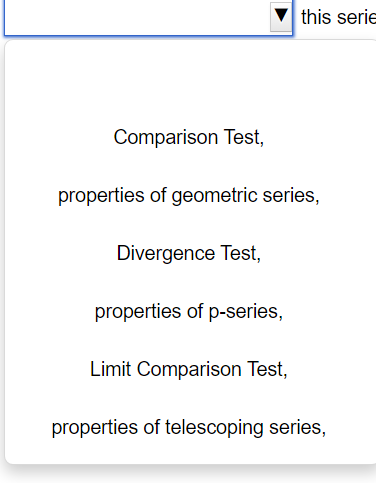
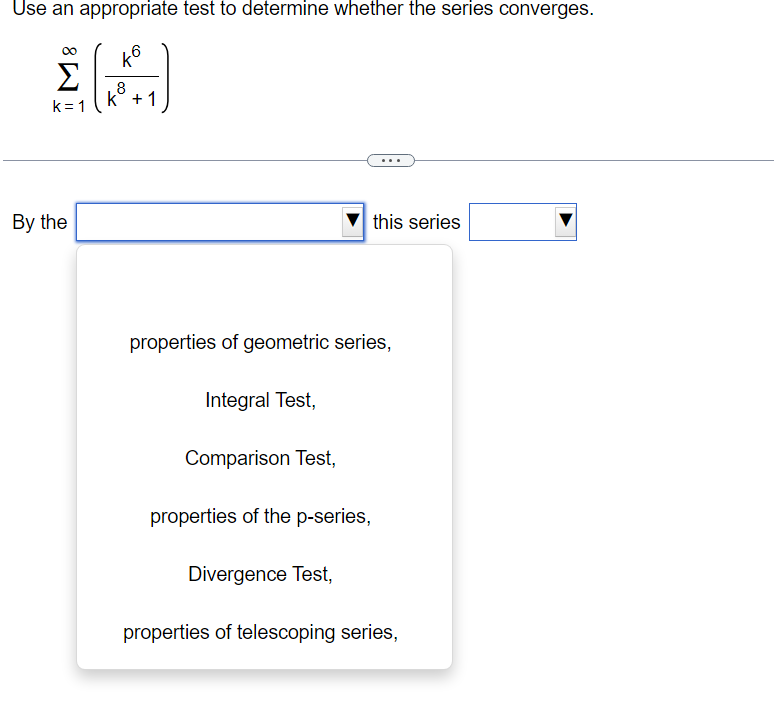
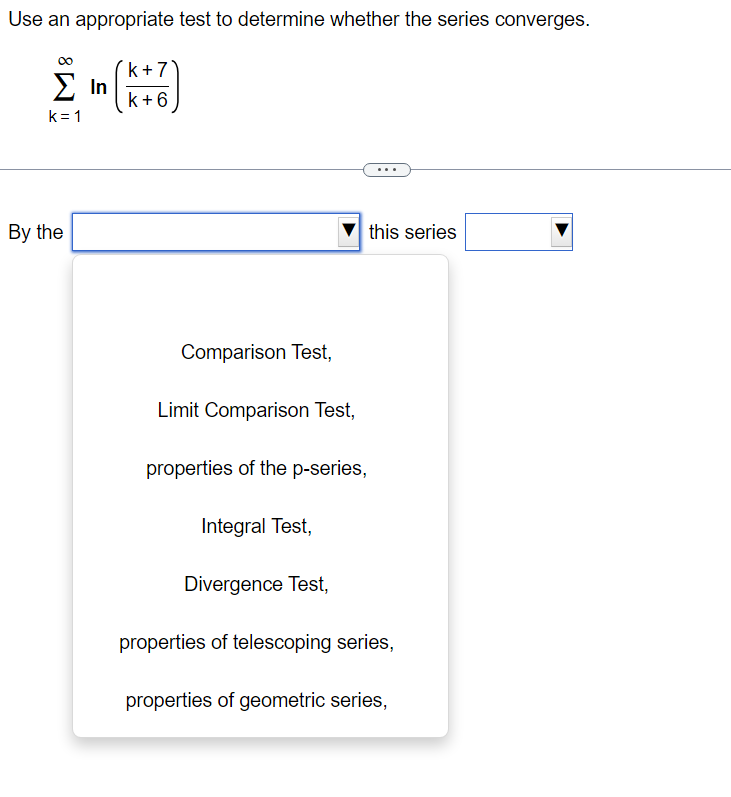
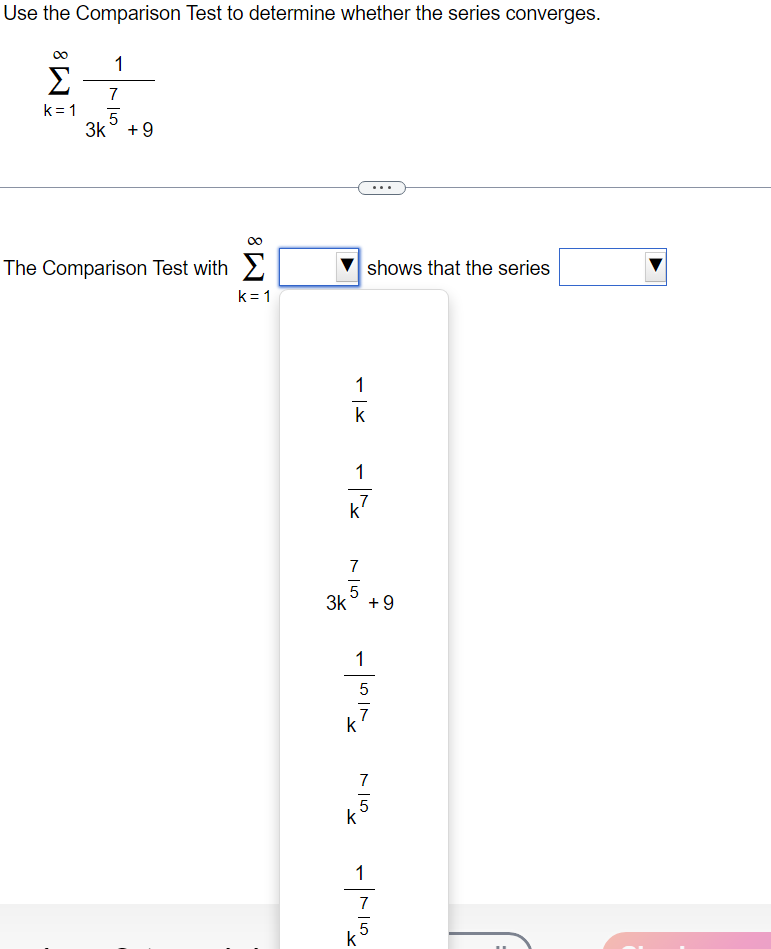
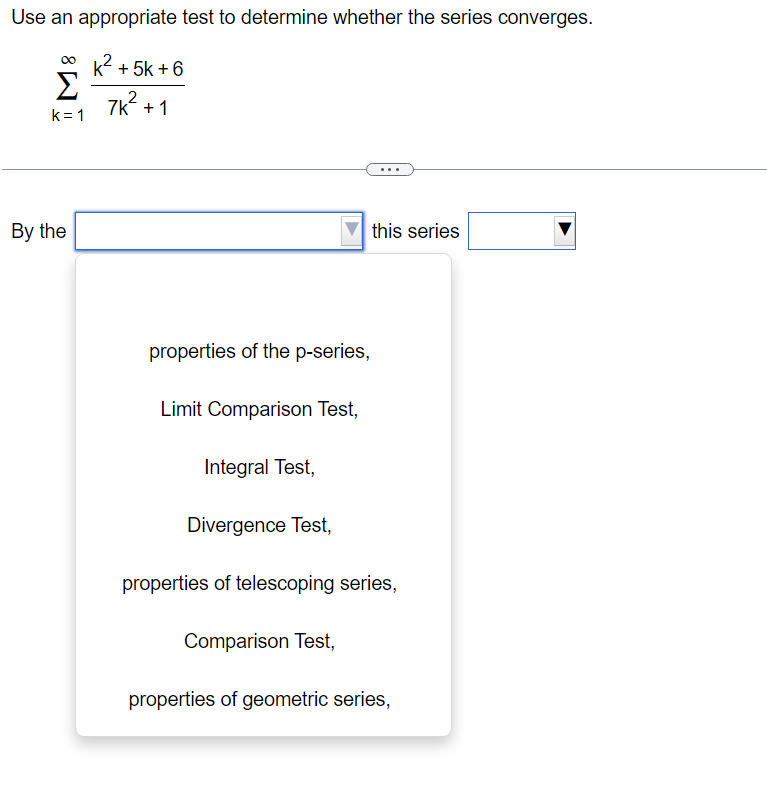
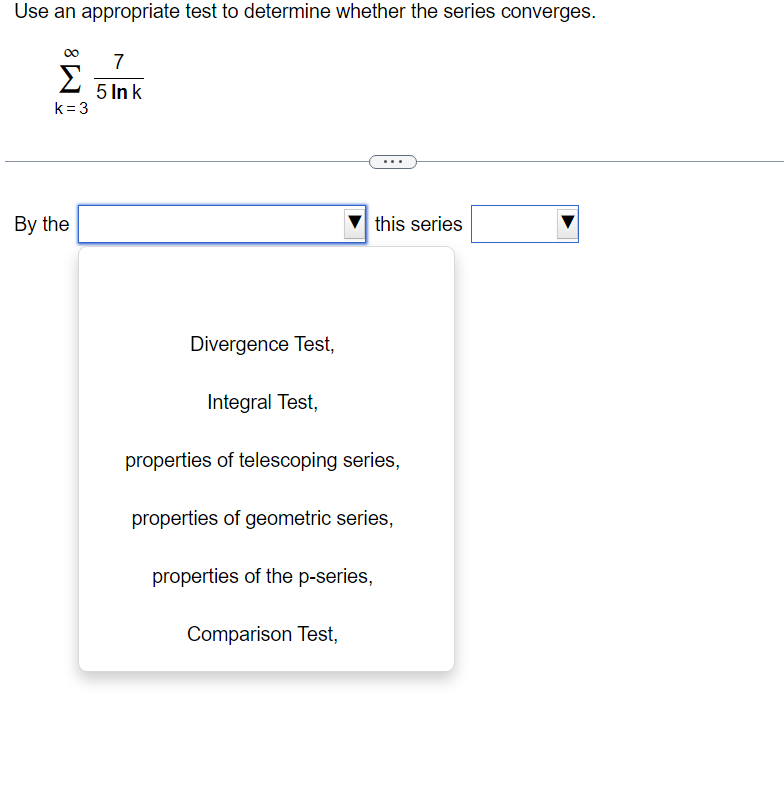
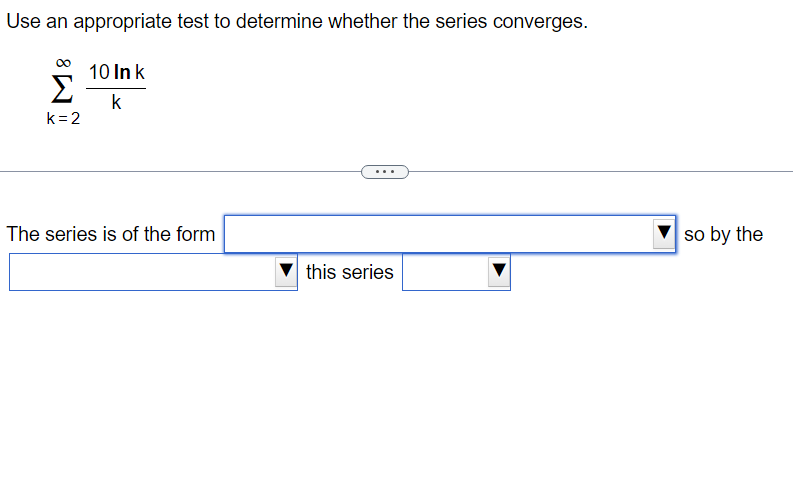
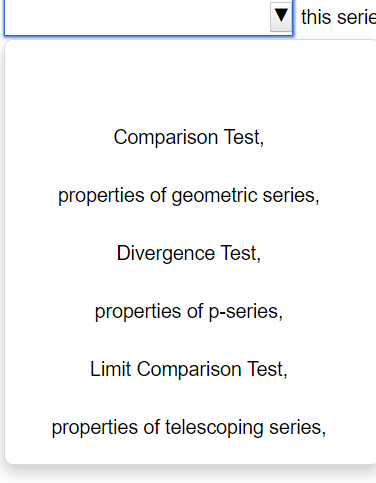
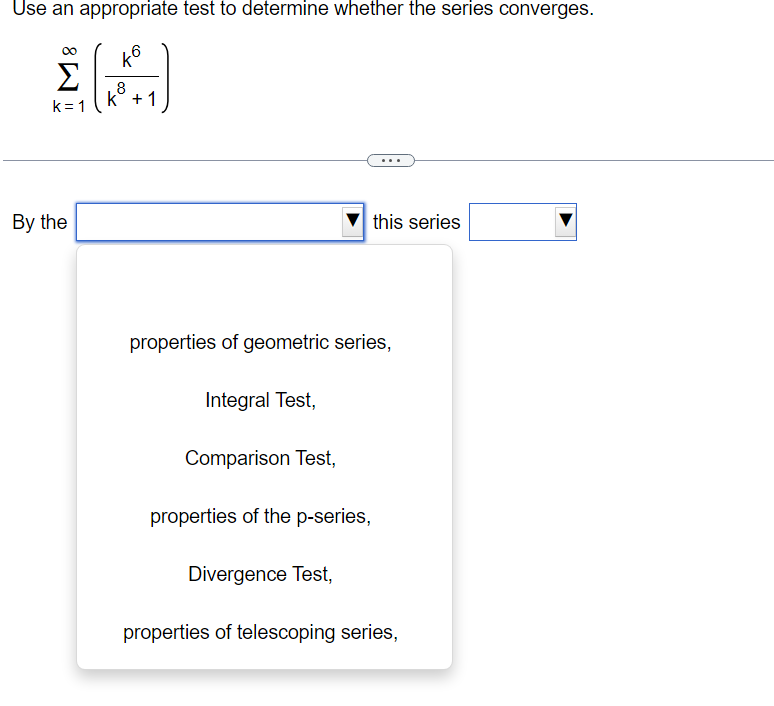
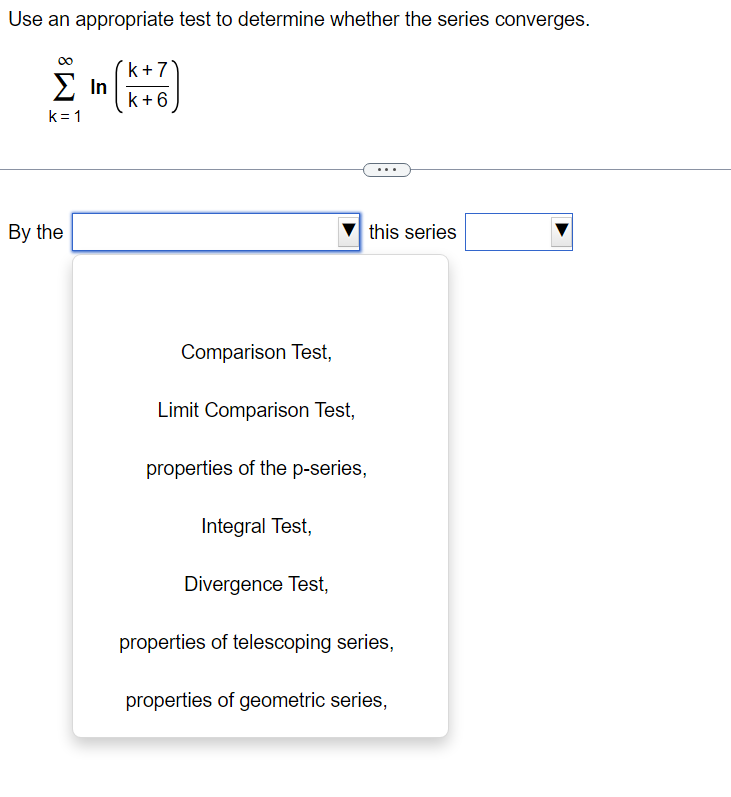
Use the Limit Comparison Test to determine whether the series converges. m k4+9 2 K21k5+5 00 The Limit Comparison Test with 2 shows that the series k=1 diverges. Use the Comparison Test to determine whether the series converges. k = 1 3k + 9 . . . The Comparison Test with shows that the series k = 1 3k + 9Use the Comparison Test to determine whether the series converges. oo sin [3] E1 k4 Choose the correct answer below. 00 [:3 A. The Comparison Test with 2 k4 shows that the series diverges. K21 1 ("3. B. The Comparison Test with Z 4 shows that the series diverges. " _ k ki DO [:3 c_ The Comparison Test with z k4 shows that the series converges. k=1 1 [:3 D. The Comparison Test with Z k4 shows that the series converges. K=1 Use an appropriate test to determine whether the series converges. By the | this series Y properties of the p-series, Limit Comparison Test, Integral Test, Divergence Test, properties of telescoping series, Comparison Test, properties of geometric series, Use an appropriate test to determine whether the series converges. co 7 5 In k K = 3 By the this series Divergence Test, Integral Test, properties of telescoping series, properties of geometric series, properties of the p-series, Comparison Test,Use an appropriate test to determine whether the series converges. 10 Ink E k k = 2 The series is of the form so by the this seriesDO f(k) for appropriate f and f(x) dx converges, k = 1 Z ak where 0