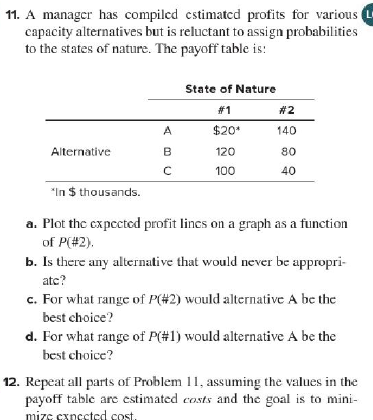
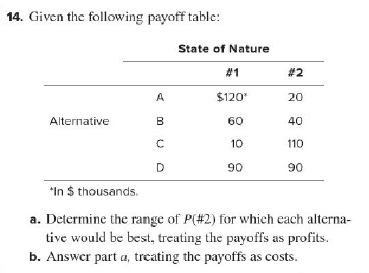
11. A manager has compiled estimated profits for various capacity alternatives but is reluctant to assign probabilities to the states of nature. The payoff table is: State of Nature #1 #2 $20* 140 A Alternative B 120 80 100 40 "In $ thousands. a. Plot the expected profit lines on a graph as a function of P(#2), b. Is there any alternative that would never be appropri- ate? c. For what range of P(#2) would alternative A be the best choice? d. For what range of P(#1) would alternative A be the best choice? 12. Repeat all parts of Problem 11, assuming the values in the payoff table are estimated costs and the goal is to mini- mize cxpccted cost. 3. A company that plans to expand its product line must decide whether to build a small or a large facility to produce the new products. If it builds a small facility and demand is low, the net present value after deducting for building costs will be $400,000. If demand is high, the company can either maintain the small facility or expand it. Expansion would have a net present value of $450,000, and maintaining the small facility would have a net present value of $350,000. If a large facility is built and demand is high, the esti- mated net present value is $800,000. If demand turns out to be low, the net present value will be -$10,000. The probability that demand will be high is estimated to be 0.60, and the probability of low demand is estimated to be 0.40. a. Analyze this decision problem using a decision tree. b. Draw the risk profile (for the better alternative). c. Calculate the EVPI. How could this information be used? d. Determine the range of P(demand low) over which each alternative would be better. e. Use an exponential utility with risk tolerance R= $300,000 to evaluate this problem. 14. Given the following payoff table: State of Nature #1 #2 A $120 20 Alternative B 60 40 10 110 D 90 90 "In $ thousands a. Determine the range of P(#2) for which each alterna- tive would be best, treating the payoffs as profits. b. Answer part a, treating the payoffs as costs. 18. The board of governors of Santa Clara University is contem- plating mandatory testing of its student athletes. The test is not 100 percent accurate. The conditional probabilities are as follows: If an athlete uses drugs, then the test will be positive 94 percent of the time, whcrcas if he does not (i.c., he is a non- uscr), the test will be negativc 98 percent of the time. Suppose the board suspects that 4 percent of the athletes use drugs. a. Calculate the posterior probabilities (i.e., probability of correct identification after a drug test). b. If a test costs $50, the cost of not identifying (and bar- ring) a drug user is $1,000, the cost of falsely accusing a non-user is $100, and other costs are zero, should the university test any athlete? Draw and use a decision trec