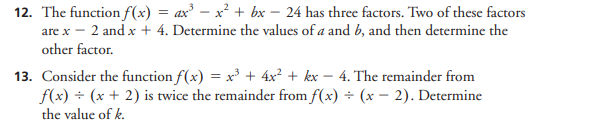
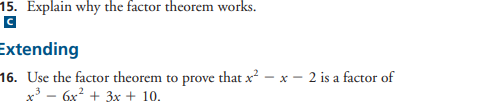
12. The function f(x) = ax' - x' + bx - 24 has three factors. Two of these factors are x - 2 and x + 4. Determine the values of a and 6, and then determine the other factor. 13. Consider the function f(x) = x' + 4x2 + kx - 4. The remainder from f(x) + (x + 2) is twice the remainder from f(x) + (x - 2). Determine the value of k.15. Explain why the factor theorem works. C Extending 16. Use the factor theorem to prove that x - x - 2 is a factor of x3 - 6x2 + 3x + 10.4. State the remainder when x + 2 is divided into each polynomial. Ka) x+ 7 x+9 d) x - 2x3 - 11x3 + 10x - 2 b) 6x3 + 19x3 + 11x - 11 e) x + 3x - 10x + 6 c) x* - 5x3 + 4 f) 4x* + 12x - 13x2 - 33x + 18 5. Determine whether 2x - 5 is a factor of each polynomial. a) 2x3- 5x2 - 2x + 5 c) 2x4 - 7x3- 13x2 + 63x - 45 b) 3x + 2x2 - 3x - 2 d) 6x4 + x - 7x - x+ 1 6. Factor each polynomial using the factor theorem. a) x - 3x' - 10x + 24 d) 4x' + 7x3- 80x2 - 21x + 270 b) 4x + 12x2 - x - 15 e) x - 5x - 7x + 29x3+ 30x c) x' + 8x + 4x2 - 48x f) xi+ 2x - 23x2 - 24x + 144 7. Factor fully. a) f(x) = x'+9x2 + 8x -60 d) f(x) = x'+ 3x3 - 38x2 + 24x + 64 b) f(x) = x - 7x - 6 e) f( x) = x-x+x-1 c) f(x) = x- 5x2+ 4 f) f(x) = x' - x + 2x3 - 2x' + x- 1 8. Use the factored form of f(x) to sketch the graph of each function in question 7. 9. The polynomial 12x' + kx - x - 6 has 2x - 1 as one of its factors. Determine the value of k. 10. When ax' - x' + 2x + b is divided by x - 1, the remainder is 10. When it is A divided by x - 2, the remainder is 51. Find a and b.1. a) Givenf(x) = x + 5x) + 3x- - 7x + 10, determine the remainder when f(x) is divided by each of the following binomials, without dividing. i) x - 2 ii) x + 4 iii) x - 1 b) Are any of the binomials in part a) factors of f(x)? Explain. 2. Which of the following functions are divisible by x - 1? a) f(x) = x- 15x + 2x-+ 12x - 10 b) g(x) = 5x3 - 4x3 + 3x - 4 c) b(x) = x4 - 7x3+ 2x2 + 9x d) j(x) = x - 1