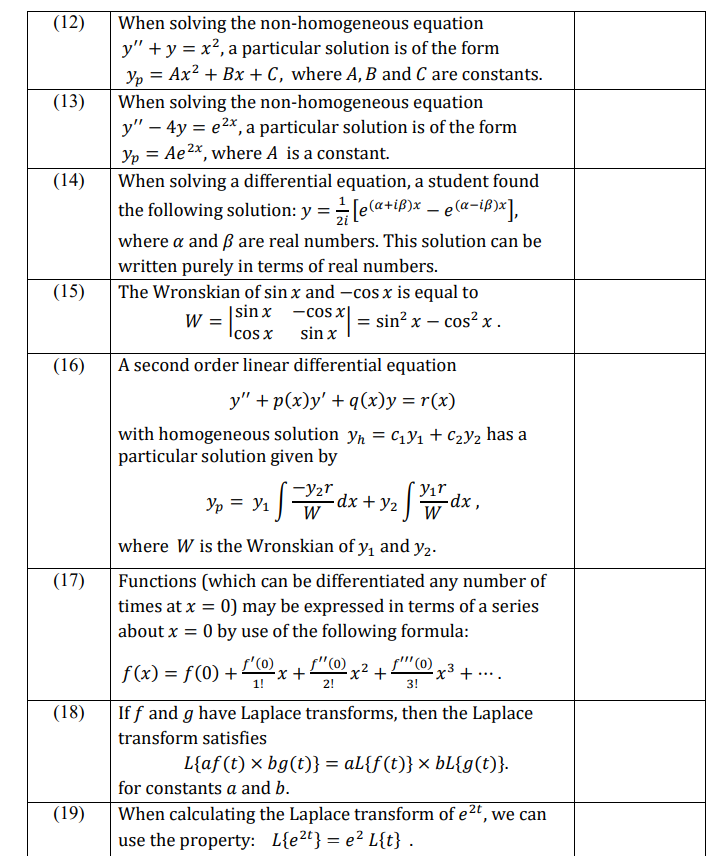
(12) When solving the non-homogeneous equation y" + y = x2, a particular solution is of the form Vp = Ax' + Bx + C, where A, B and C are constants. (13) When solving the non-homogeneous equation y" - 4y = ex, a particular solution is of the form Vp = Aex, where A is a constant. (14) When solving a differential equation, a student found the following solution: y = = [e(atip)x - e(a-ip)x], where a and B are real numbers. This solution can be written purely in terms of real numbers. (15) The Wronskian of sin x and -cos x is equal to W = |sin x -cos x = sin2 x - cos? x . cos x sin x (16) A second order linear differential equation y" + p(x)y' + q(x)y= r(x) with homogeneous solution yn = C171 + C232 has a particular solution given by Vp = Vi wdx + yz Vir wdx , where W is the Wronskian of y, and y2. (17) Functions (which can be differentiated any number of times at x = 0) may be expressed in terms of a series about x = 0 by use of the following formula: f(x) =f(0)+x+/2x2 + 1"@ 2! 3! -x3 +.... (18) If f and g have Laplace transforms, then the Laplace transform satisfies Laf (t) x bg(t)} = al{f (t)} x bLig(t)}. for constants a and b. (19) When calculating the Laplace transform of e , we can use the property: Lie?} = e? L{t]