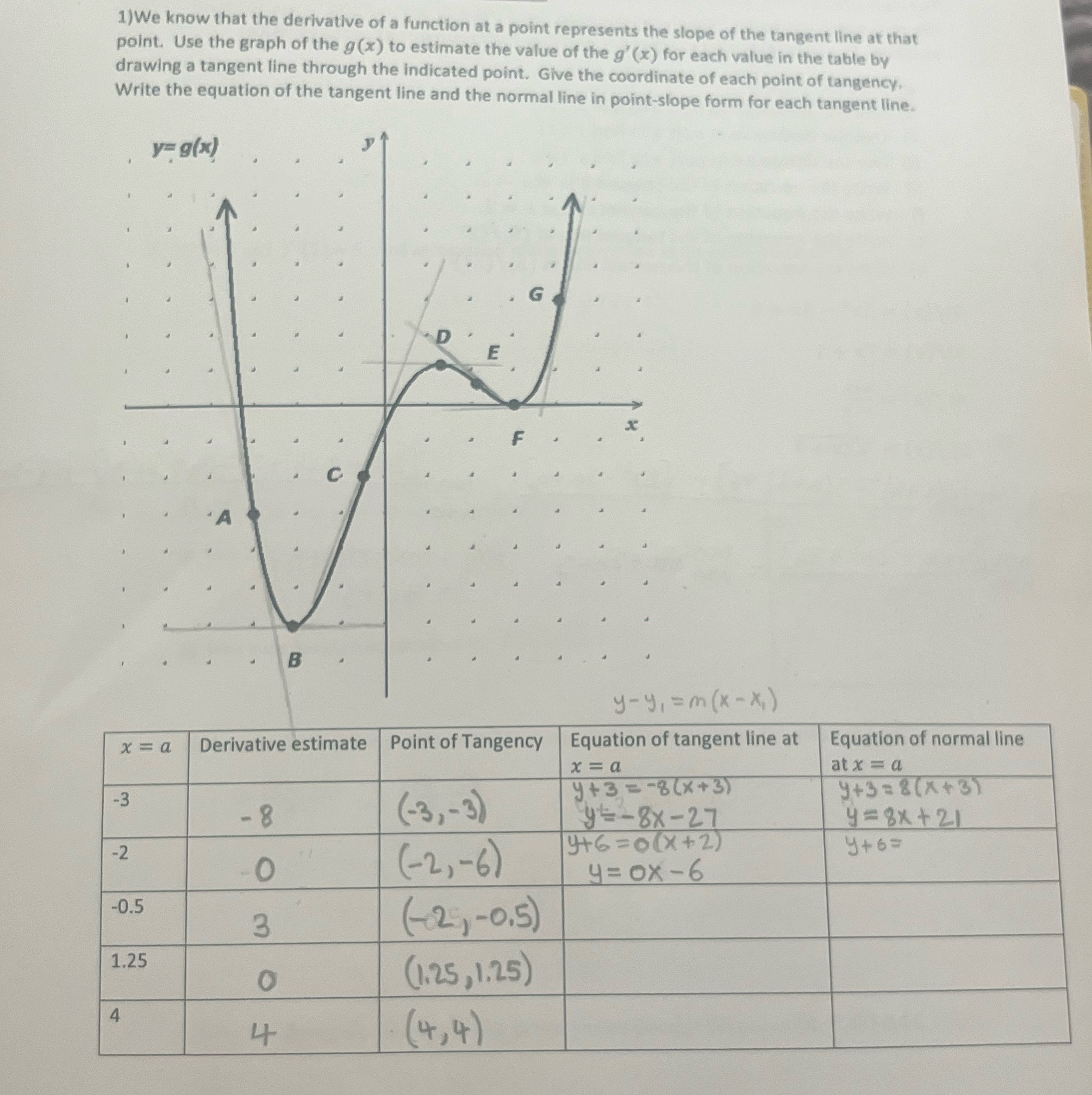
1)We know that the derivative of a function at a point represents the slope of the tangent line at that point. Use the graph of the g(x) to estimate the value of the g'(x) for each value in the table by drawing a tangent line through the indicated point. Give the coordinate of each point of tangency. Write the equation of the tangent line and the normal line in point-slope form for each tangent line. y= g(x) A B D E F G 14 y-y = m (x-x) x = a Derivative estimate Point of Tangency Equation of tangent line at -3 -8 -2 -O (-3,-3) (-2,-6) 3 -0.5 1.25 0 4 (-2,-0.5) (1.25,1.25) (4,4) x = a Y+3=-8(x+3) y=-8x-27 9+6=0(x+2) y=0x-6 Equation of normal line at x = a Y+3=8(x+3) y=8x+21 Y+6=