Answered step by step
Verified Expert Solution
Question
1 Approved Answer
2. 3. 4. 5. Consider the polynomial function P(r)= 9(r6) (r + 7)(r - 2). - The roots of P(x) are and their multipicities are
![Consider the polynomial function [ P(r)=-9(r-6)^{4}(r+7)^{6}(r-2) ] The roots of ( P(x) ) are , and their multipicities a](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/04/6440cbffe580f_1681968126708.jpg)
2.
3.
4.
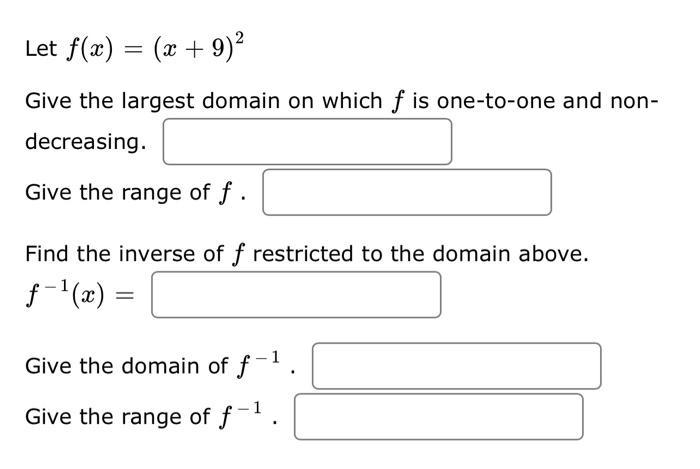
5.
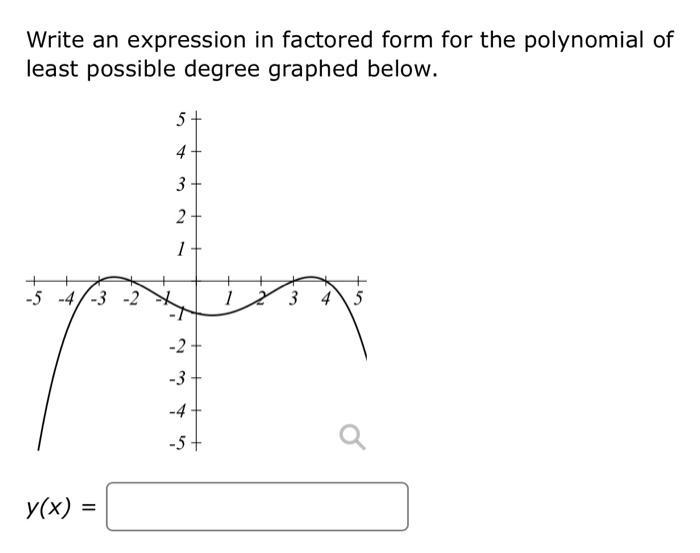
Consider the polynomial function P(r)= 9(r6) (r + 7)(r - 2). - The roots of P(x) are and their multipicities are List the values separated by commas. For example, "1,2,3,4". The degree of P(x) is
Step by Step Solution
★★★★★
3.47 Rating (154 Votes )
There are 3 Steps involved in it
Step: 1
1 The polynomial Pr is already given in the factored form So the roots will be obtained by equating each factor to zero The roots are r 6 0 implies r 6 r 7 0 implies r 7 r 2 0 implies r 2 The multipli...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Introduction To Probability And Statistics
Authors: William Mendenhall, Robert J. Beaver, Barbara M. Beaver
13th Edition
0495389536, 9780495389538
