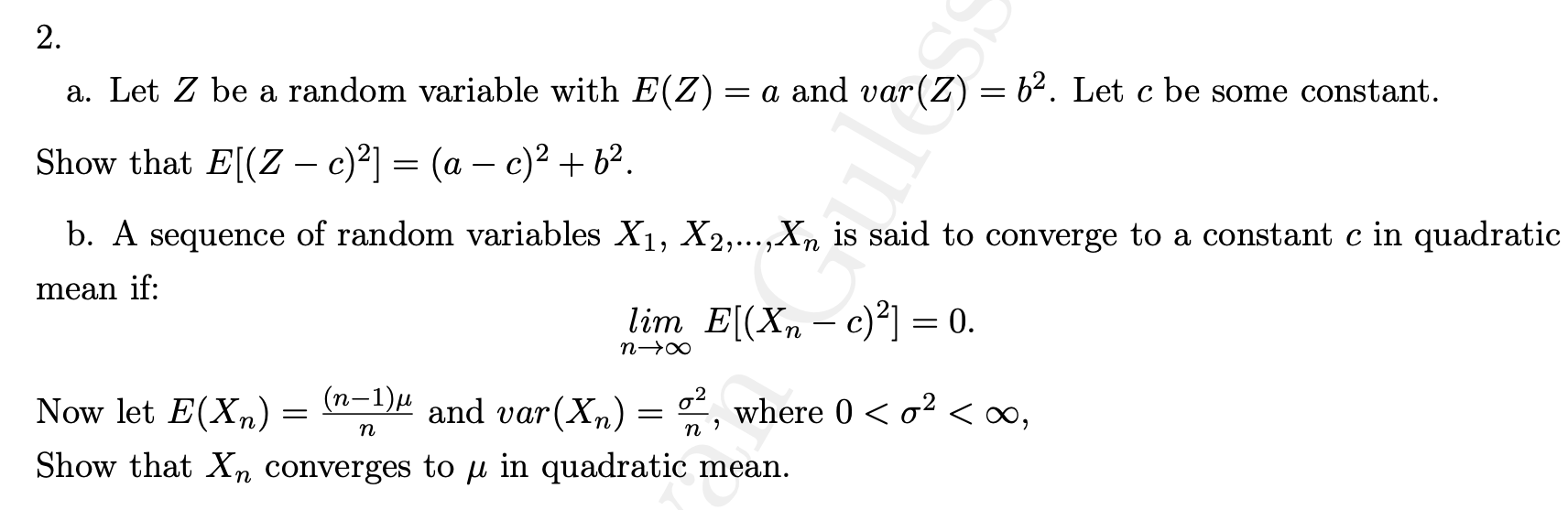
2. a. Let Z be a random variable with E(Z) = a and var(Z) = b2. Let c be some constant. Show that E[(Z - c)2] = (a - c)2+ 62. b. A sequence of random variables X1, X2,...,Xn is said to converge to a constant c in quadratic mean if: lim E[(Xn - c) 2] = 0. Now let E(Xn) = (n-1)u n and var (Xn) = 02 n , where 0