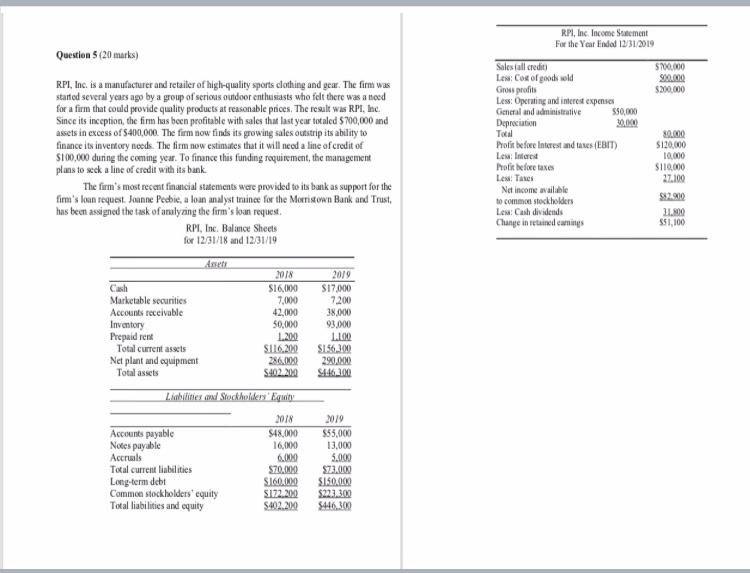
2. At this point, we can analyze (stability, steady-state gain, sinusoidal steady-state gains, time-constant, etc.) of first-order, linear dynamical systems. We previously analyzed a Ist-order process model, and a proportional-control strategy. In this problem, we try a different situation, where the process is simply proportional, but the controller is a Ist-order, linear dynamical system. Specifically, suppose the process model is non-dynamic ("static" ) simply y(t) = cu(t) + Bd(t) where o and B are constants. The control strategy is dynamic i (t) = ar(t) + bir(t) + bzym(t) u(t) = cr(t) + dir(t) where ym(t) = y(t) + n(t) and the various "gains" (a, bi, . .., di) constitute the design choices in the control strategy. Be careful, notation-wise, since (for example) d, is a constant parameter, and d(t) is a signal (the disturbance). (a) Eliminate u and ym from the equations to obtain a differential equation for r of the form r(t) = Ar(t) + Bir(t) + Bad(t) + Ban(t) which governs the closed-loop behavior of r. Note that A, B1, B2, By are functions of the parameters a, b1, ... in the control strategy, as well as the process parameters o and B. (b) What relations on (a, b1. .... dj, or, B) are equivalent to closed-loop system stability? (c) As usual, we are interested in the effect (with feedback in place) of (r, d, n) on (y, u), the regulated variable, and the control variable, respectively. Find the coefficients (in terms of (a, bi, . . ., d1, 0, B)) so that y(t) = Cix(t) + Dur(t) + Died(t) + Dian(t) u(t) = Car(t) + Dar(t) + Dad(t) + Dzan(t) (d) Suppose that T. > 0 is a desired closed-loop time constant. Write down the constraints on the a, b1, b2, c and di (i.e., the parameters of the controller to be design) such that the following conditions hold: . closed-loop is stable . closed-loop time constant is To . steady-state gain from d -> y is 0 . steady-state gain from r - y is 12. At this point, we can analyze (stability, steady-state gain, sinusoidal steady-state gains, time-constant, etc.) of first-order, linear dynamical systems. We previously analyzed a Ist-order process model, and a proportional-control strategy. In this problem, we try a different situation, where the process is simply proportional, but the controller is a Ist-order, linear dynamical system. Specifically, suppose the process model is non-dynamic ("static" ) simply y(t) = cu(t) + Bd(t) where o and B are constants. The control strategy is dynamic i (t) = ar(t) + bir(t) + bzym(t) u(t) = cr(t) + dir(t) where ym(t) = y(t) + n(t) and the various "gains" (a, bi, . .., di) constitute the design choices in the control strategy. Be careful, notation-wise, since (for example) d, is a constant parameter, and d(t) is a signal (the disturbance). (a) Eliminate u and ym from the equations to obtain a differential equation for r of the form r(t) = Ar(t) + Bir(t) + Bad(t) + Ban(t) which governs the closed-loop behavior of r. Note that A, B1, B2, By are functions of the parameters a, b1, ... in the control strategy, as well as the process parameters o and B. (b) What relations on (a, b1. .... dj, or, B) are equivalent to closed-loop system stability? (c) As usual, we are interested in the effect (with feedback in place) of (r, d, n) on (y, u), the regulated variable, and the control variable, respectively. Find the coefficients (in terms of (a, bi, . . ., d1, 0, B)) so that y(t) = Cix(t) + Dur(t) + Died(t) + Dian(t) u(t) = Car(t) + Dar(t) + Dad(t) + Dzan(t) (d) Suppose that T. > 0 is a desired closed-loop time constant. Write down the constraints on the a, b1, b2, c and di (i.e., the parameters of the controller to be design) such that the following conditions hold: . closed-loop is stable . closed-loop time constant is To . steady-state gain from d -> y is 0 . steady-state gain from r - y is 1R.PI, Inc. Income Statement For the Year Endal 1231/2019 Question 5 (20 marks) Sales fall credit 5740.030 Los: Cost of goods cold RPI, Inc. is a manufacturer and retailer of high-quality sports clothing and gear. The firm was Gross profits started several years ago by a group of serious outdoor enthusiasts who fell there was a need Less: Operating and intered expenses for a firm that could provide quality products at reasonable prices, The result was RPI. Inc. General and administrative Since its inception, the firm has been profitable with sales that last year totaled $700,000 and Depreciation assets in excess of 5400,000. The firm now finds its growing sales outstrip its ability to Total finance its inventory needs. The firm now estimates that it will need a line of credit of Profit before Interest and taxes (EBIT) $100,000 during the coming year. To finance this funding requirement, the management Lew: Inand plans to seek a line of credit with its bank. Profit before taxes $110,100 Lew: Taxes 27.100 The firm's most recent financial statements were provided to its bank as support for the Net income available firm's loan request. Joanne Peebie, a loan analyst traince for the Morristown Bank and Trust, to common stockholders 5:2 900 has been assigned the task of analyzing the firm's loan request. Lew: Cash dividenda RPI, Inc. Balance Sheets Change in retained earnings $51,100 for 12/31/18 and 12/31/19 JO18 2019 Cash $16.030 $17,000 Marketable securities 7.00.0 7,200 Accounts receivable 42,000 38,000 Inventory 50.000 93.000 Prepaid rent 1.20:0 L.LOO Total current assets $116.200 $156 300 Net plant and equipment 286.000 290.0.00 Total assets $402 20 0 Limbifities ood Stockholders Equity Accounts payable $48.000 $55.000 Notes payable 16.000 13,000 Accruals 6.004 5.000 Total current liabilities $70.00-0 $73.0100 Long-term debt $160.000 $1502000 Common stockholders* equity $ 172. 20.0 $221300 Total liabilities and equity 5402.200 $463mQuestion 2 (25 Points). Trade: The tables below describe two differ ent cases of production costs for pharmaceutical products and machinery in Switzerland and Italy. The numbers in the table indicate the number of workers required for a unit of production. The variable a: is the wage in Switzerland relative to Italy. For instance, to = 1 means that the wage is identical in both countries while it; = 1.5 means that the wage in Switzerland is 50% higher. Case 1: Cost of Making a Unit of a Good Pharmaceutical products Machinery Switzerland 4 a w 8 a: to Italy 19 10 Case 2: Cost of Making a Unit of a Good Pharmaceutical products Machinery Switzerland 8 at w 4 =l= w Italy 19 10 o For each case, show which products one should expect to be produced in Switzerland and which products one should expect to be produced in Italy (both countries will export part of their produced goods to the other country). Use the concept of comparative advantage. o For each case, determine the possible range of w in a trade equilibrium, that is, the range of m such that each country produces exactly one of the goods, and each good is produced in the country which has a lower production cost for it. (Note: to pin down the exact wage w, we would also need to know the labOr supply, but this is not required here.) a In which of the two cases would you expect larger gains from trade