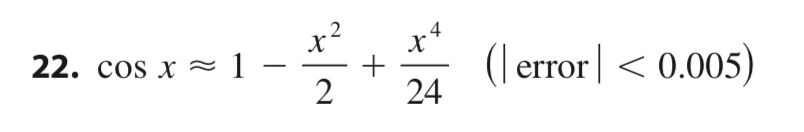
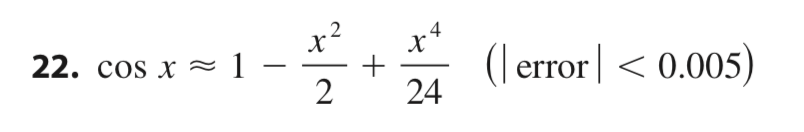
20. Suppose you know that ( l)\" n! {n} 4 = f ( ) 3\"(n + l) and the Taylor series of f centered at 4 converges to f (x) for all x in the interval of convergence. Show that the fth- degree Taylor polynomial approximates f (5) with error less than 0.0002. @ 2122 I Use the Alternating Series Estimation Theorem or Taylor's Formula to estimate the range of values of x for which the given approximation is accurate to within the stated error. Check your answer graphically.