26. The first step in the decision-making process of chapter 7, is to identify and define the problem.

27. Creativity is one of our greatest personal assets, even though it may not be recognized.

28. Step 3 of the decision-making process, making a decision, is the easiest of the four steps in this process.

29. The Mount Everest case in chapter 7, illustrates the do ethical reasoning for all of the steps of the decision-making process.

30. Self-confidence means you do not need others as team members to succeed at work.

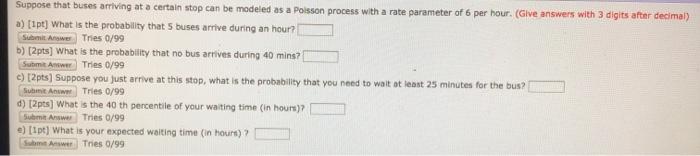
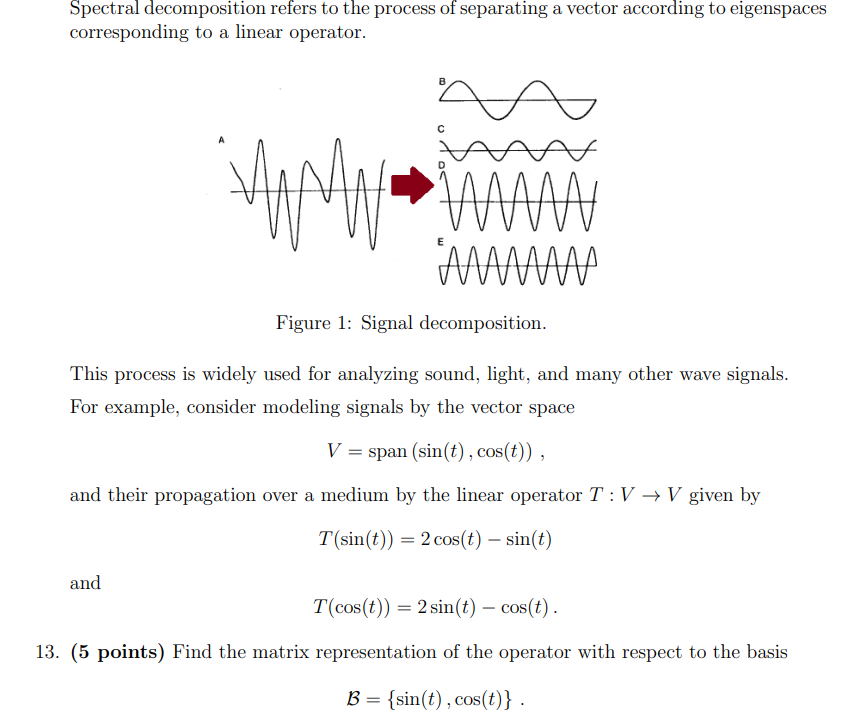
Suppose that buses arriving at a certain stop can be modeled as a Poisson process with a rate parameter of 6 per hour. (Give answers with 3 digits after decimal) a) [1pt] What is the probability that 5 buses arrive during an hour? Submit Answer. Tries 0/99 b) [2pts] What is the probability that no bus arrives during 40 mins? Submit Amver Tries 0/99 c) [2pts] Suppose you just arrive at this stop, what is the probability that you need to wait at least 25 minutes for the bus? Submit Apoem Tries 0/99 d) [2pts] What is the 40'th percentile of your waiting time (In hours]? Subma Arwer Tries 0/99 e) [1pt] What is your expected waiting time (in hours) ? Submit Answer Tries 0/99Spectral decomposition refers to the process of separating a vector according to eigenspaces corresponding to a linear operator. 0 A M Do U i U U 6 Figure 1: Signal decomposition. This process is widely used for analyzing soundJ light? and many other wave signals. For example1 consider modeling signals by the vector space V = span [sin(t) ,cos[t)) , and their propagation over a medium by the linear operator T : V > V given by T(sin{t)) = 2cos{t) sin(t) and T(cos(t)) = 2 sin(t) cos(t) . 13. (5 points} Find the matrix representation of the operator with respect to the basis 3 = {sin(t) ,cos(t)} . 1. Determine the mean-square value of the random process with spectral density defined by: Sx (w) = 1 - 2. Consider a random process with spectral density Sx (@)). The process has mean-square value of 4. Determine the mean-square values of random processes having the following spectral densities: a) 25x(w) b) Sx (2() c) Sx(w/2) 3. Consider a stationary random process with spectral density defined as: Sx(w) = 3216(w) + 876(w - 3) + 876(w + 3) + 32no(w -6) + 32no(w +6) a) What is the mean value of this process? b) What is the variance of this process? c) What are the discrete frequencies of this process