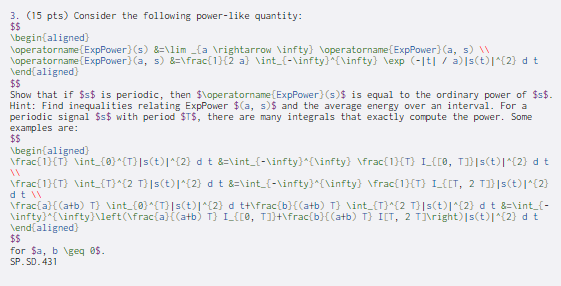
$$ $$ 3. (15 pts) Consider the following power-like quantity: \begin{aligned) \operatorname[ExpPower}(s) &=\lim _{a ightarrow \infty) \operatorname[ExpPower)(a, 5) W operatorname[ExpPower) Ca, s) &=\frac{1}2 a} \int _{-\infty}^{\infty} \exp(-1t| / a) s(+)["{2}d t \end{aligned} Show that if $s$ is periodic, then $\operatorname[ExpPower}(s)$ is equal to the ordinary power of $s$. Hint: Find inequalities relating ExpPower $ca, s) and the average energy over an interval. For a periodic signal $s$ with period $T$, there are many integrals that exactly compute the power. Some examples are: $$ \begin{aligned] \frac{1}{T} \int_{0}^{T}|s(t)|^{2} d t &=\int_{-\infty}^{\infty} \frac{1}T) I_{[0, 1]}|s(t)|^{2}dt \frac{1}{T} \int_{T}^{2 T}|s(t)]^{2} d t &=\int_{-\infty }^{\infty} \frac{1}{T} I_{[T, 2 T1}|s(t)^{2} dt \frac{a}{(atb) T} \int_{0)^{}{s(t)^{2}d t+\frac{b} Catb) T} \int_{T}^{2 T}|s(t)^{2) d t 8=\int_{- \infty}^{\infty}\left(\frac{a}(a+b) T} I_{[e, T]}+\frac{b}{(a+b) T] IT, 2 Ti ight)|s(t)^{2} dt \end{aligned $$ for $a, b \geq 05. SP.SD.431