3. Consider a portfolio choice problem with a risk-free asset with return 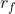and two risky assets, the first with mean return 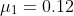and standard deviation 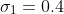and the second with mean 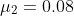and standard deviation 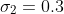, with correlation 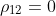. For any stock portfolio let denote the proportion invested in stock 1 . (a) Find the weight that minimizes portfolio standard deviation 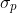. (b) Consider the tangency portfolio and let 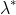denote the weight it places on stock 1 . Find the condition that defines this value, but do not solve for it, and explain how it would compare to 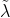. (c) Now consider varying the risk-free rate 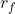. Again, without solving anything, explain how you would expect 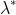to vary as 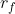increases. (d) Show how the slope of the tangent line changes with 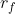. Recall a useful theorem that allows you to do this without ever actually solving for 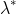. (e) Suppose instead that 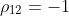so that the stocks always move against each other. Find the weight 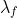that yields a risk-free portfolio and the expected return 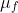to this portfolio.