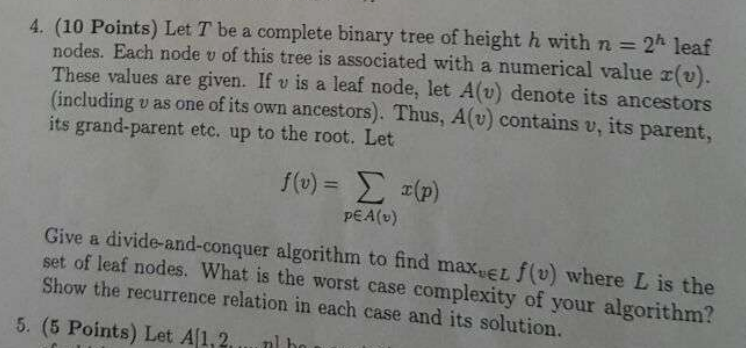
4. (10 Points) Let T be a complete binary tree of height h with n = 2h leaf nodes. Each node v of this tree is associated with a numerical value x(u). These values are given. If v is a leaf node, let A(v) denote its ancestors (including v as one of its own ancestors). Thus, A(u) contains v, parent, its grand-parent etc. up to the root. Let f(u)= x(p) PEA(U) v, its Give a divide-and-conquer algorithm to find max el f(u) where L is the set of leaf nodes. What is the worst case complexity of your algorithm? Show the recurrence relation in each case and its solution. 5. (5 Points) Let A[1,2. ml 4. (10 Points) Let T be a complete binary tree of height h with n = 2h leaf nodes. Each node v of this tree is associated with a numerical value x(u). These values are given. If v is a leaf node, let A(v) denote its ancestors (including v as one of its own ancestors). Thus, A(u) contains v, parent, its grand-parent etc. up to the root. Let f(u)= x(p) PEA(U) v, its Give a divide-and-conquer algorithm to find max el f(u) where L is the set of leaf nodes. What is the worst case complexity of your algorithm? Show the recurrence relation in each case and its solution. 5. (5 Points) Let A[1,2. ml