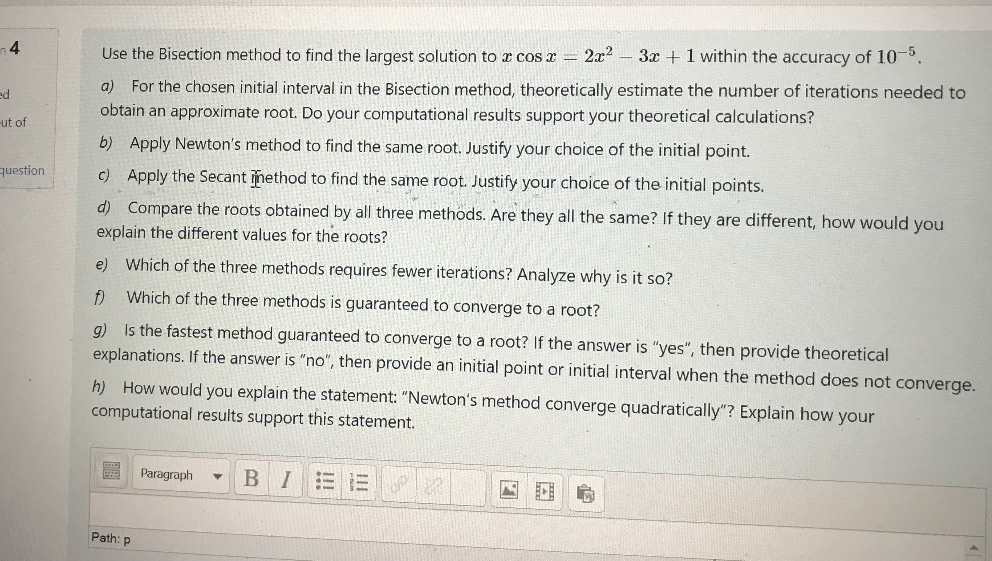
4 Use the Bisection method to find the largest solution to a cos x - 2x- - 3x + 1 within the accuracy of 10-5. a) For the chosen initial interval in the Bisection method, theoretically estimate the number of iterations needed to ad obtain an approximate root. Do your computational results support your theoretical calculations? ut of b) Apply Newton's method to find the same root. Justify your choice of the initial point. question c) Apply the Secant method to find the same root. Justify your choice of the initial points. d) Compare the roots obtained by all three methods. Are they all the same? If they are different, how would you explain the different values for the roots? e) Which of the three methods requires fewer iterations? Analyze why is it so? f) Which of the three methods is guaranteed to converge to a root? g) Is the fastest method guaranteed to converge to a root? If the answer is "yes", then provide theoretical explanations. If the answer is "no", then provide an initial point or initial interval when the method does not converge. h) How would you explain the statement: "Newton's method converge quadratically"? Explain how your computational results support this statement. Paragraph B Path: p