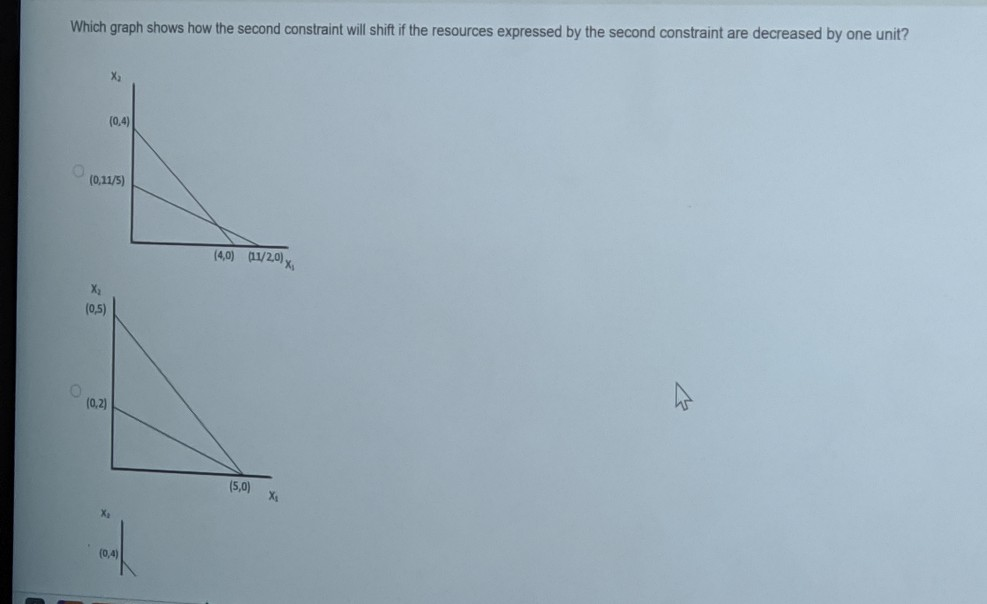
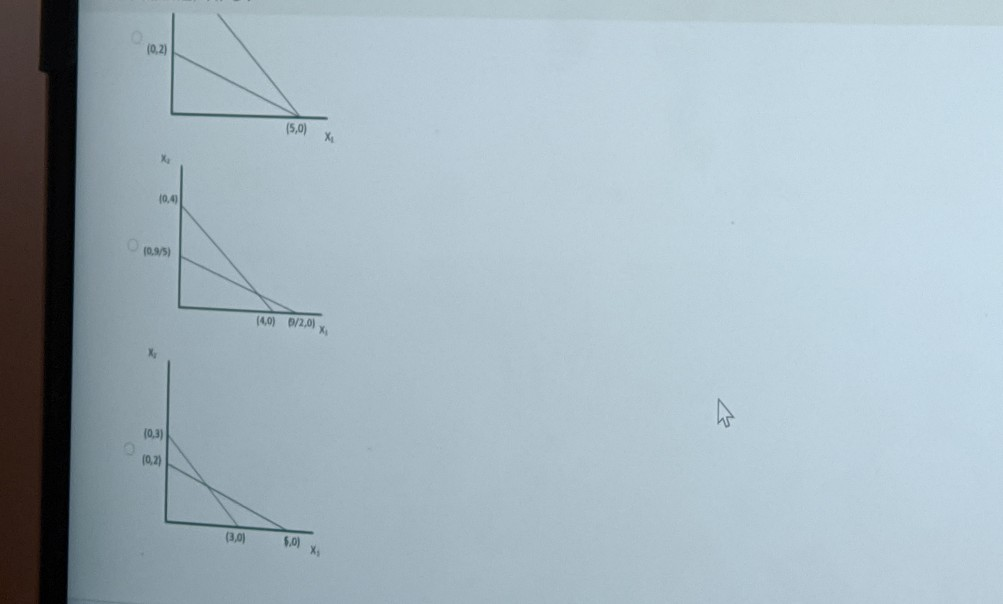
41 Consider the following linear programming formulation: Max Z = X1 + X2 Subject to X + X 54 2X1 +5X2 5 10 Xq, X20 The feasible region is shown in the graph: X (0,4) 10,2) (4,0) 6.0) X Which graph shows how the second constraint will shift if the resources expressed by the second constraint are decreased by one unit? X . (0,4) Which graph shows how the second constraint will shift if the resources expressed by the second constraint are decreased by one unit? X (0.4) (0,11/5) (4,0) 01/2.0) X, 10,5) (0,2) (5,0) X X (0,4) Izol lo's) X 10.4 Iseol (4,0) 0/2,0) leol 10,2) lo's) lo's X 42 Consider the following linear programming formulation: Min Z = X1 + X2 Subject to X + X2 24 2X1 +5X22 10 3x + X 56 X, X20 The feasible region is shown in the graph: X 06 10:22 2,0 140) 6,01 X If the resources expressed by the third constraint are unlimited (infinite resources), how does the constraint shift in the graph, and how does the shift affect the problem? The third constraint shifts to the right, and it no longer binds the problem. The third constraint remains in the same position, but the feasible area changes. The third constraint shifts to the left, and it no longer binds the problem The third constraint shifts to the right, and there is no longer a feasible area. The third constraint shifts to the left, and the feasible area increases. A NEXT > BOOKMARK CLEAR