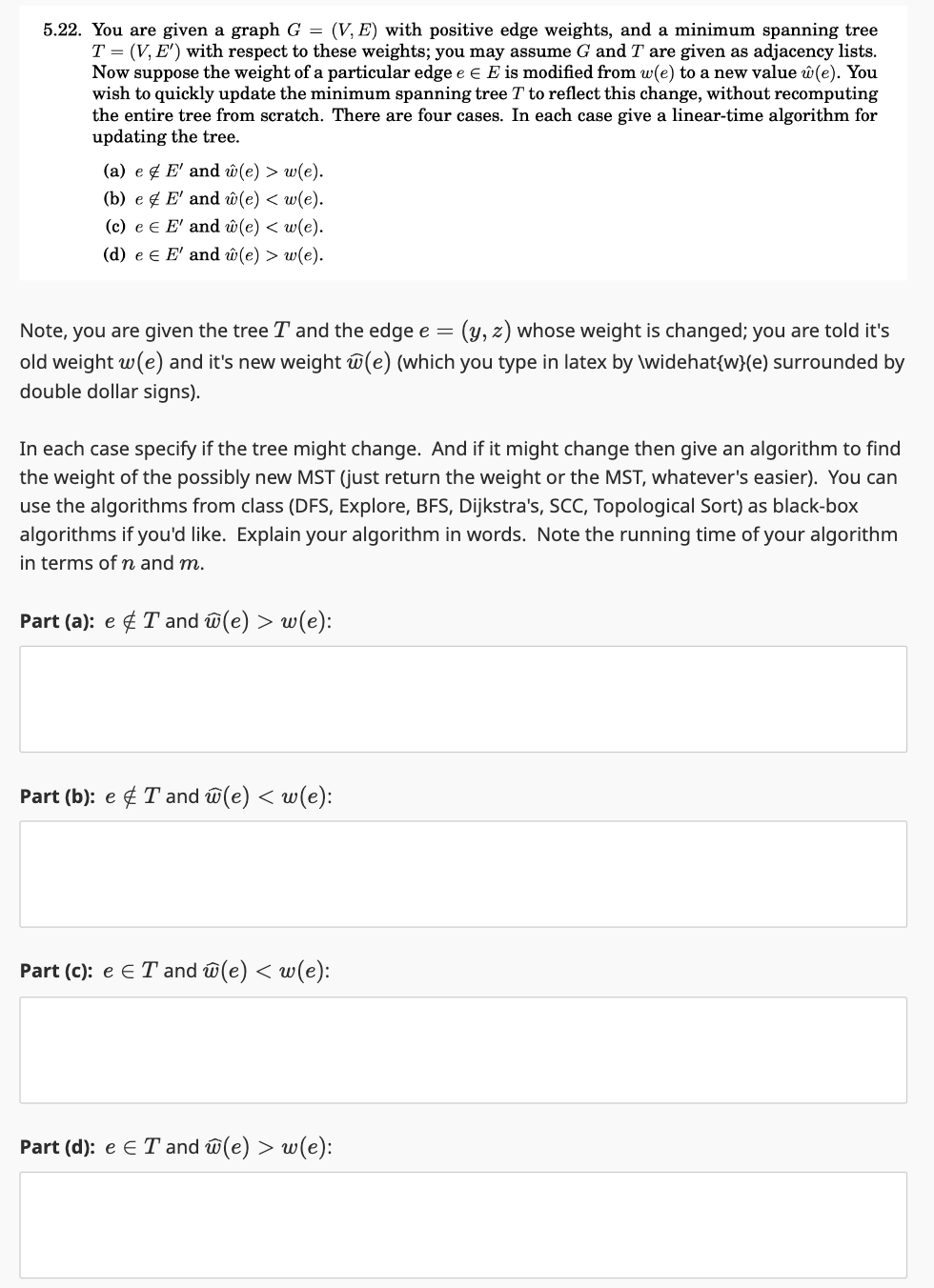
Question: 5 . 2 2 . You are given a graph G = ( V , E ) with positive edge Note, you are given the
You are given a graph with positive edge Note, you are given the tree and the edge whose weight is changed; you are told it's
old weight and it's new weight widehatwhich you type in latex by Iwidehat surrounded by
double dollar signs
In each case specify if the tree might change. And if it might change then give an algorithm to find
the weight of the possibly new MST just return the weight or the MST whatever's easier You can
use the algorithms from class DFS Explore, BFS Dijkstra's, SCC Topological Sort as blackbox
algorithms if you'd like. Explain your algorithm in words. Note the running time of your algorithm
in terms of and
Part a: inT and widehat :weights, and a minimum spanning tree You are given a graph with positive edge weights, and a minimum spanning tree
with respect to these weights; you may assume and are given as adjacency lists.
Now suppose the weight of a particular edge einE is modified from to a new value hat You
wish to quickly update the minimum spanning tree to reflect this change, without recomputing
the entire tree from scratch. There are four cases. In each case give a lineartime algorithm for
updating the tree.
a and hat
b and hat
with respect to these weights; you may assume and are given as adjacency lists.
Now suppose the weight of a particular edge einE is modified from to a new value hat You
wish to quickly update the minimum spanning tree to reflect this change, without recomputing
the entire tree from scratch. There are four cases. In each case give a lineartime algorithm for
updating the tree.
a and hat
b and hat
and hathat
and hat
and hat You are given a graph with positive edge weights, and a minimum spanning tree
with respect to these weights; you may assume and are given as adjacency lists.
Now suppose the weight of a particular edge einE is modified from to a new value hat You
wish to quickly update the minimum spanning tree to reflect this change, without recomputing
the entire tree from scratch. There are four cases. In each case give a lineartime algorithm for
updating the tree.
a and hat
b and hat
and hathat
and hat
and hatNote, you are given the tree and the edge whose weight is changed; you are told it's
old weight and it's new weight widehatwhich you type in latex by Iwidehat surrounded by
double dollar signs
In each case specify if the tree might change. And if it might change then give an algorithm to find
the weight of the possibly new MST just return the weight or the MST whatever's easier You can
use the algorithms from class DFS Explore, BFS Dijkstra's, SCC Topological Sort as blackbox
algorithms if you'd like. Explain your algorithm in words. Note the running time of your algorithm
in terms of and
Part a: inT and widehat :
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


