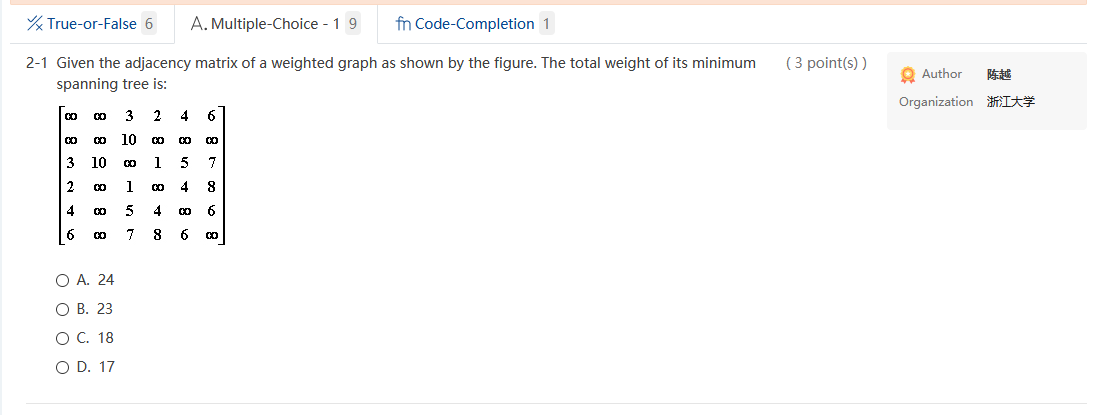
Question: i need all answer soonly. thanks True-or-False 6 A. Multiple-Choice - 19 for Code-Completion 1 (3 point(s)) 2-1 Given the adjacency matrix of a weighted
 i need all answer soonly. thanks
i need all answer soonly. thanks
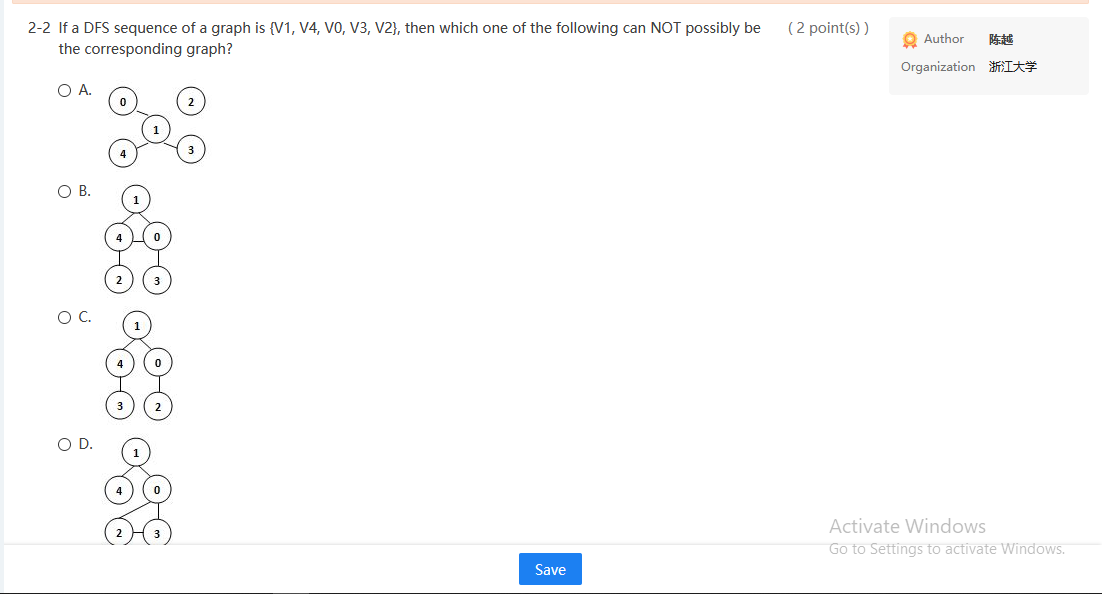
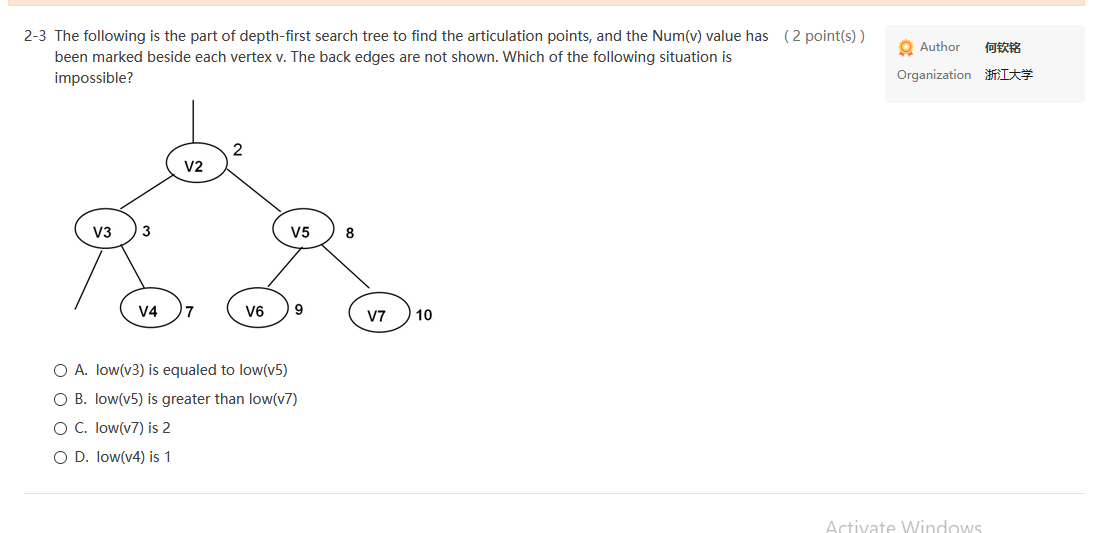
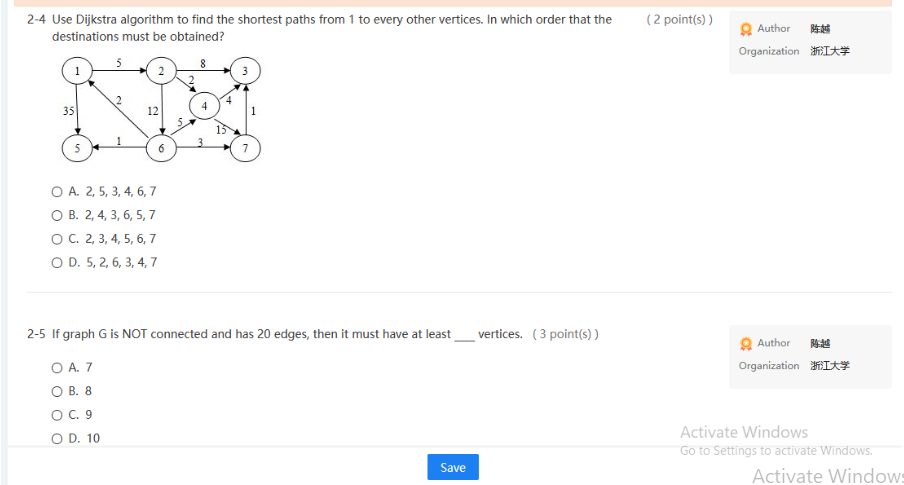
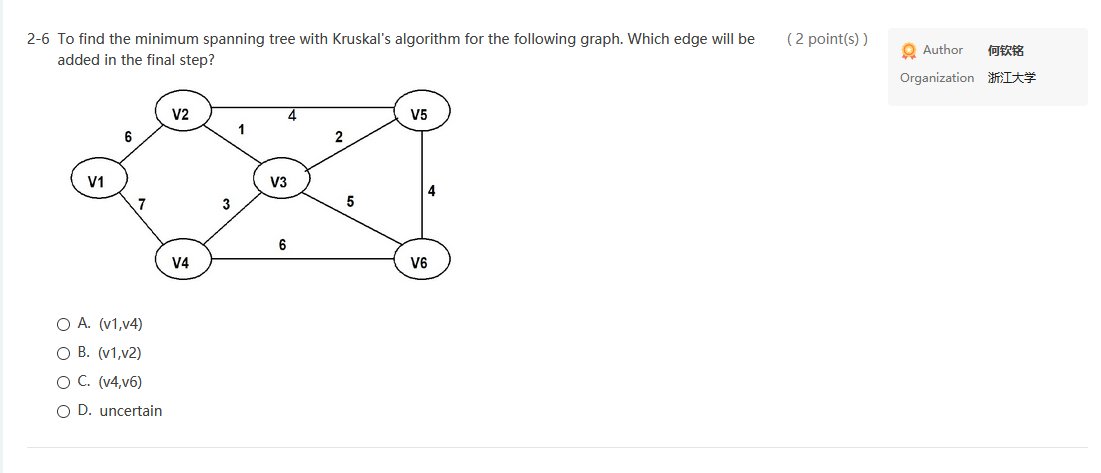
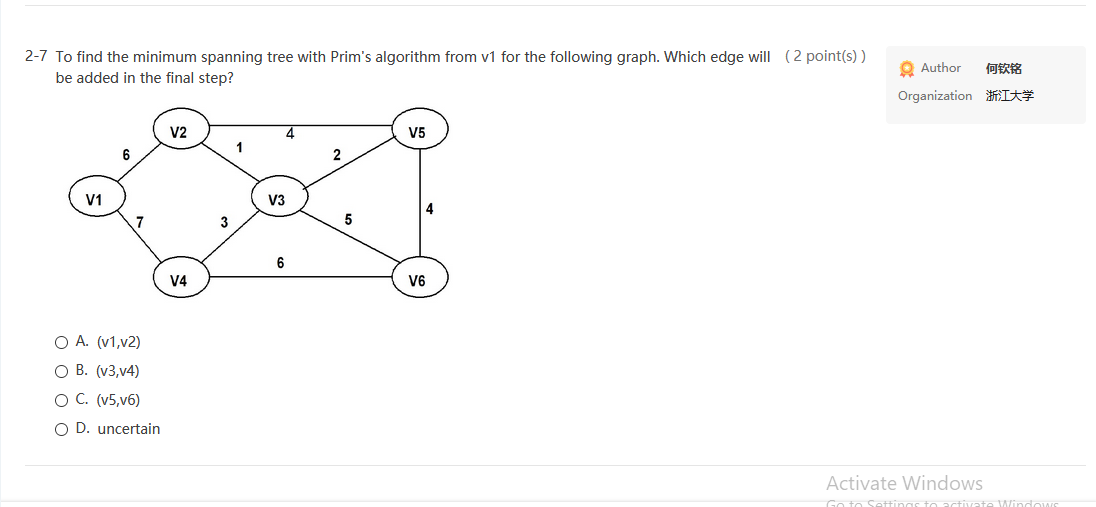
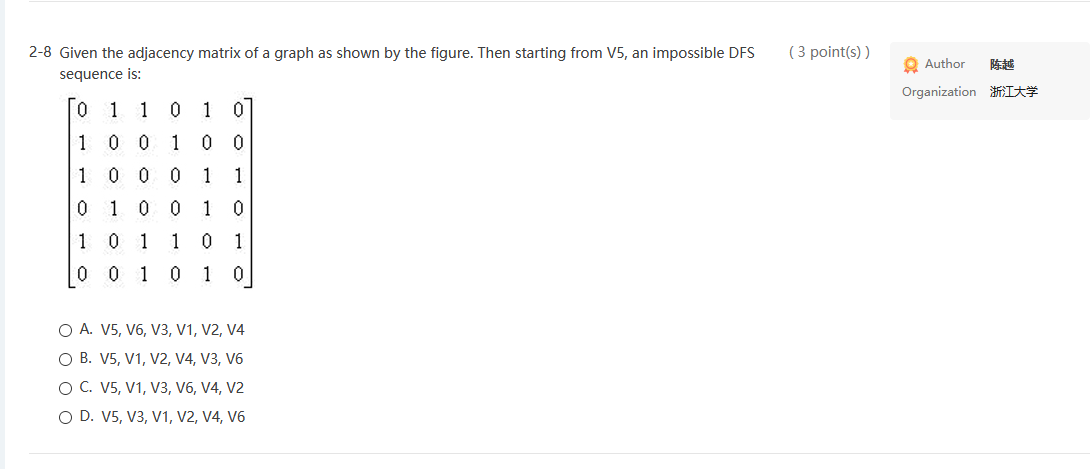
True-or-False 6 A. Multiple-Choice - 19 for Code-Completion 1 (3 point(s)) 2-1 Given the adjacency matrix of a weighted graph as shown by the figure. The total weight of its minimum spanning tree is: Author Organization It* 3 2 6 CO 10 CO co co 3 100 1 5 7 2 co 1 0 4 8 0 5 4 0 6 6 00 7 8 6 O A. 24 O B. 23 O C. 18 OD. 17 (2 point(s)) 2-2 If a DFS sequence of a graph is {V1, V4, VO, V3, V2}, then which one of the following can NOT possibly be the corresponding graph? Author Organization * OA. OB. OC. Activate Windows Go to Settings to activate Windows, Save Author 2-3 The following is the part of depth-first search tree to find the articulation points, and the Num(v) value has (2 point(s)) been marked beside each vertex v. The back edges are not shown. Which of the following situation is impossible? Organization It 2 V2 V3 3 V5 8 V4 7 V6 9 V7 10 O A. low(v3) is equaled to low(v5) O B. low(v5) is greater than low(17) O C. low(v7) is 2 O D. low(v4) is 1 Activate Windows 2-4 Use Dijkstra algorithm to find the shortest paths from 1 to every other vertices. In which order that the destinations must be obtained? (2 point(s)) Author 346 Organization I 5 3 35 12 4 13 6 7 O A. 2,5, 3, 4, 6,7 O B. 2,4,3,6,5,7 O C. 2, 3, 4, 5, 6, 7 OD. 5, 2, 6, 3, 4,7 2-5 If graph G is NOT connected and has 20 edges, then it must have at least vertices. (3 point(s)) Author 14:44 Organization in O A. 7 OB. 8 O C. 9 OD. 10 Activate Windows Go to Settings to activate Windows. Activate Windows Save (2 points) 2-6 To find the minimum spanning tree with Kruskal's algorithm for the following graph. Which edge will be added in the final step? Author OTERIS Organization ti V2 4 V5 1 6 2 V1 V3 7 3 5 6 14 V6 O A. (v1,v4) O B. (v1,v2) O C. (v4,v6) OD. uncertain 2-7 To find the minimum spanning tree with Prim's algorithm from v1 for the following graph. Which edge will (2 point(s)) be added in the final step? Author Organization V2 4 V5 1 6 2 V1 V3 7 3 5 6 V4 V6 O A. (v1,v2) O B. (v3,64) O C. (v5,6) O D. uncertain Activate Windows Go to Settings to activate Wing (3 point(s)) Author Organization I 2-8 Given the adjacency matrix of a graph as shown by the figure. Then starting from V5, an impossible DFS sequence is: [0 1 1 0 1 0 100100 100011 0 1 0 0 1 0 1 0 1 1 0 1 LO 0 1 0 1 0 O A. V5, V6, V3, V1, V2, V4 O B. V5, V1, V2, V4, V3, V6 OC. V5, V1, V3, V6, V4, V2 OD. V5, V3, V1, V2, V4, V6 2-9 The minimum spanning tree of any connected weighted graph (3 point(s)) Author Organization It* O A. must be unique O B. must have a unique minimum weight OC. must not be unique OD. may not exist Activate Windows True-or-False 6 A. Multiple-Choice - 19 for Code-Completion 1 (3 point(s)) 2-1 Given the adjacency matrix of a weighted graph as shown by the figure. The total weight of its minimum spanning tree is: Author Organization It* 3 2 6 CO 10 CO co co 3 100 1 5 7 2 co 1 0 4 8 0 5 4 0 6 6 00 7 8 6 O A. 24 O B. 23 O C. 18 OD. 17 (2 point(s)) 2-2 If a DFS sequence of a graph is {V1, V4, VO, V3, V2}, then which one of the following can NOT possibly be the corresponding graph? Author Organization * OA. OB. OC. Activate Windows Go to Settings to activate Windows, Save Author 2-3 The following is the part of depth-first search tree to find the articulation points, and the Num(v) value has (2 point(s)) been marked beside each vertex v. The back edges are not shown. Which of the following situation is impossible? Organization It 2 V2 V3 3 V5 8 V4 7 V6 9 V7 10 O A. low(v3) is equaled to low(v5) O B. low(v5) is greater than low(17) O C. low(v7) is 2 O D. low(v4) is 1 Activate Windows 2-4 Use Dijkstra algorithm to find the shortest paths from 1 to every other vertices. In which order that the destinations must be obtained? (2 point(s)) Author 346 Organization I 5 3 35 12 4 13 6 7 O A. 2,5, 3, 4, 6,7 O B. 2,4,3,6,5,7 O C. 2, 3, 4, 5, 6, 7 OD. 5, 2, 6, 3, 4,7 2-5 If graph G is NOT connected and has 20 edges, then it must have at least vertices. (3 point(s)) Author 14:44 Organization in O A. 7 OB. 8 O C. 9 OD. 10 Activate Windows Go to Settings to activate Windows. Activate Windows Save (2 points) 2-6 To find the minimum spanning tree with Kruskal's algorithm for the following graph. Which edge will be added in the final step? Author OTERIS Organization ti V2 4 V5 1 6 2 V1 V3 7 3 5 6 14 V6 O A. (v1,v4) O B. (v1,v2) O C. (v4,v6) OD. uncertain 2-7 To find the minimum spanning tree with Prim's algorithm from v1 for the following graph. Which edge will (2 point(s)) be added in the final step? Author Organization V2 4 V5 1 6 2 V1 V3 7 3 5 6 V4 V6 O A. (v1,v2) O B. (v3,64) O C. (v5,6) O D. uncertain Activate Windows Go to Settings to activate Wing (3 point(s)) Author Organization I 2-8 Given the adjacency matrix of a graph as shown by the figure. Then starting from V5, an impossible DFS sequence is: [0 1 1 0 1 0 100100 100011 0 1 0 0 1 0 1 0 1 1 0 1 LO 0 1 0 1 0 O A. V5, V6, V3, V1, V2, V4 O B. V5, V1, V2, V4, V3, V6 OC. V5, V1, V3, V6, V4, V2 OD. V5, V3, V1, V2, V4, V6 2-9 The minimum spanning tree of any connected weighted graph (3 point(s)) Author Organization It* O A. must be unique O B. must have a unique minimum weight OC. must not be unique OD. may not exist Activate Windows
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


