Question: 5. Suppose that u( 3, y) is a continuously differentiable, circularly symmetric function, so that when expressed in polar coordinates, I = roos, , y

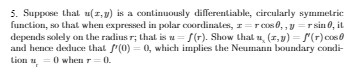
5. Suppose that u( 3, y) is a continuously differentiable, circularly symmetric function, so that when expressed in polar coordinates, I = roos, , y = rain, it depends solely on the rixliusr; that is w = / (r). Show that a (x,y) = /(r) cost and hence deduce that /(0) = 0, which implies the Neumann boundary condi- lion u = 0 when r = (

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Directions: Answer the questions below. Make sure to justify your responses. A. [10 pts] Suppose that' u = (3, a, 1) and v = (2, 4,3). Find all values of real values of a so scal - u = scale v or...

QUESTION 5 The US customs know that a drug shipment is being smuggled into the country in the baggage of an unknown passenger on one of two flights, one from Bogota and one from Cartagena. Both...

Question 1 Consider an economy with / consumers and & goods. For each consumer i e {1, ..., /}. the consumption set is R4. Her utility function is given by "(x') = - where ax, B; > 0 for k E {1. ...,...

Need answers of this problem, without expalanation, just answer (1 point) Below is a diagram of the dotted cube with edges of length 5. Suppose vectors u = (5, 0, 0), v = (0, 5, 0), and w = (0, 0,...

Macro \fassigns to EL ]. PE's beliefs are common knowledge between M and PE as is the feet that M hows the true value of 9. Thus we have s situation of ineomplete information. (d) Using the Harsanyi...

Step by step calculations QUESTION 4 Consider a market for a homogeneous good, which is produced at zero cost. Market inverse demand is given by P=1-20 (where ( is industry output). Let #, be...

HHelp in giving the correct answers 6 In a certain country, all civil servants are recruited on their 25th birthdays. (Birthdays are assumed to occur uniformly over the calendar year). Of those who...

ANSWER all questions they are micro QUESTION 1 Your entire wealth consists of the balance of your bank account, which is $ W. . You also own a painting which is worthless to you. You have a chance to...

Suppose T: R3-R2 is a linear transformation. Let U, V and W be the vectors given below, and suppose that T(U) and T(V) are as given. Find T(W). -5 14 18 U = -3 V = -2 W = 13 T(U) = T(V)= 16 19 9 T(W)...

MC G G C W V GOGG in G ( X X G B # 6 7 GALA + V X ( - C webwork.charlotte.edu/webwork2/Math2164DYs/Chapter_8/5/?effectiveUser=supreti1&tuser=supreti1&key=OxHhSz9tZLiLA2pkTSILmkrj3DuhdffM Update...

A company makes a purchase under credit terms of 1/10 net 30. At which of the following investment rates should the company be indifferent about taking the discount and paying on day 10 or forgoing...

The following data set represents the record high temperatures in degree Fahrenheit (F) for each of the 50 US states: 106 98 96 108 90 93 89 103 104 119 111 85 97 102 85 109 93 120 98 102 90 96 114...

The following statement is false in respect of capital gains tax: A ) It is a separate tax levied in addition to income tax B ) Capital losses may not be set off against revenue gains in determining...

Summerdahl Resort's common stock is currently trading at $35 a share. The stock is expected to pay a dividend of $2.50 a share at the end of the year (D1 = $2.50), and the dividend is expected to...