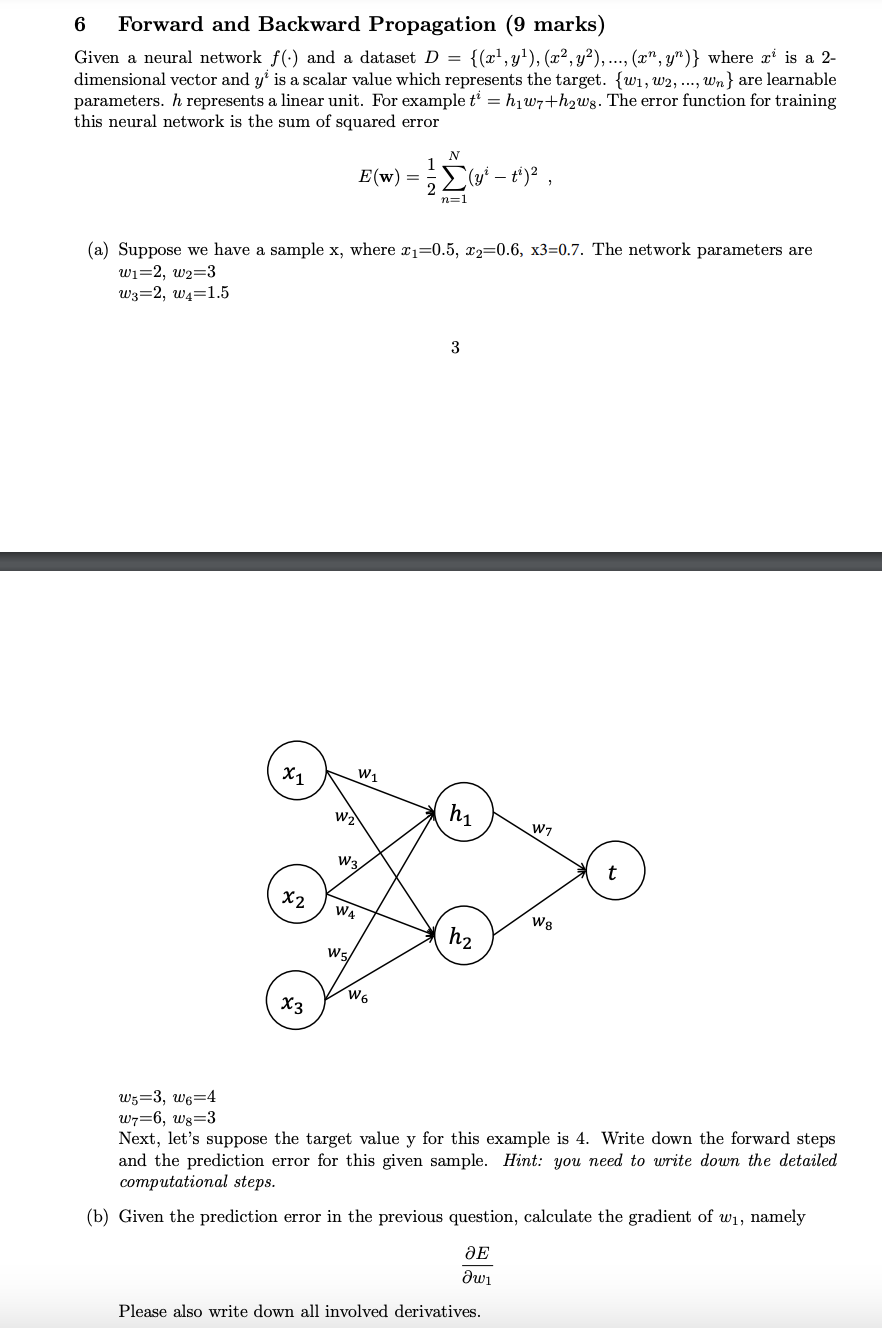
6 Forward and Backward Propagation (9 marks) Given a neural network f() and a dataset D = {(x, y), (x, y), ..., (x^, y")} where x is a 2- dimensional vector and y' is a scalar value which represents the target. {w1, W2, ..., wn} are learnable parameters. h represents a linear unit. For example t = hw7+h2w8. The error function for training this neural network is the sum of squared error N E(w)= n=1 (a) Suppose we have a sample x, where x1=0.5, x2=0.6, x3=0.7. The network parameters are W1=2, w2=3 w3=2, w4=1.5 3 W1 x1 m W7 W W3 W8 x2 WA h2 W5/ W6 X3 t w5=3, w6=4 Ww7=6, w8=3 Next, let's suppose the target value y for this example is 4. Write down the forward steps and the prediction error for this given sample. Hint: you need to write down the detailed computational steps. (b) Given the prediction error in the previous question, calculate the gradient of w, namely Jw1 Please also write down all involved derivatives.