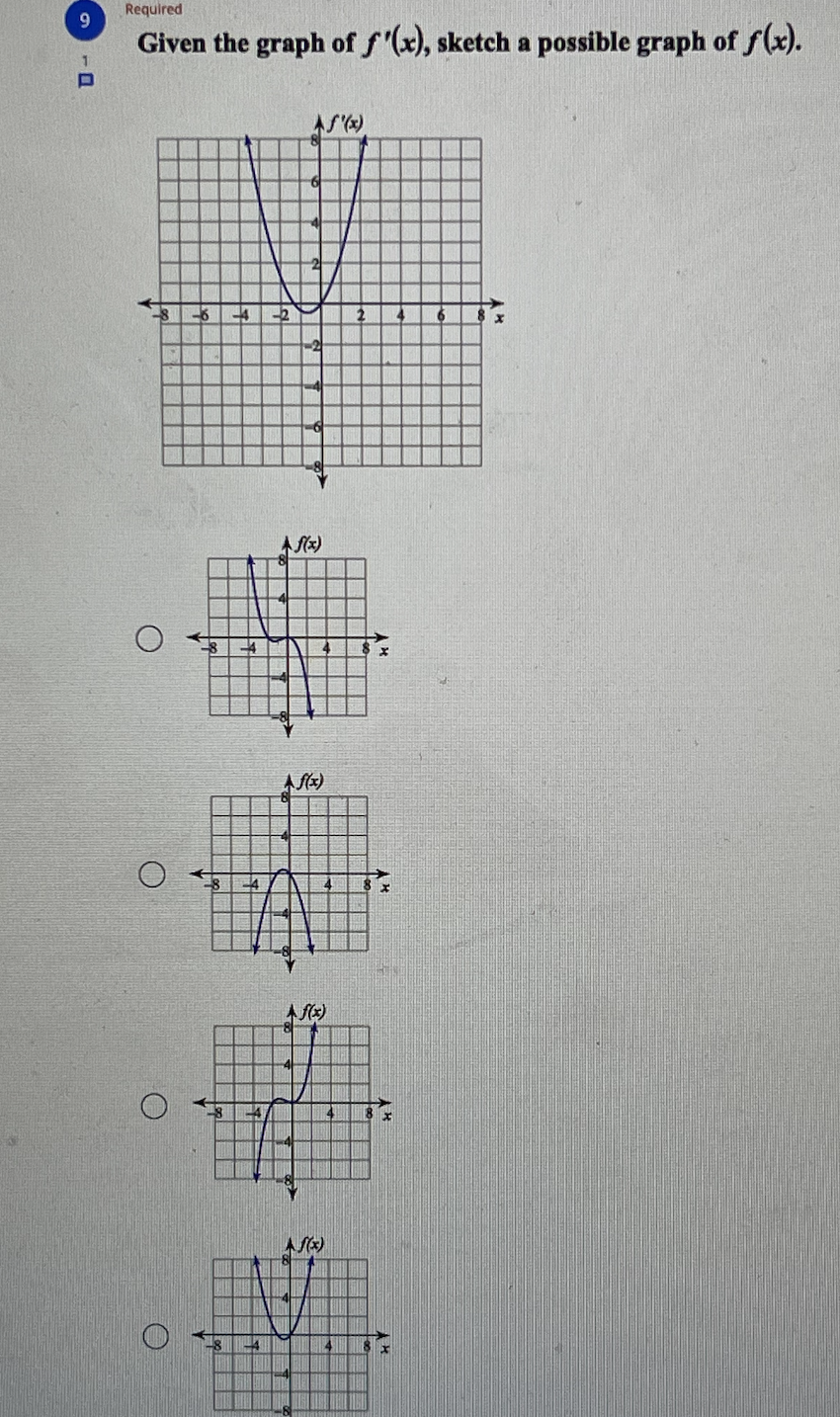
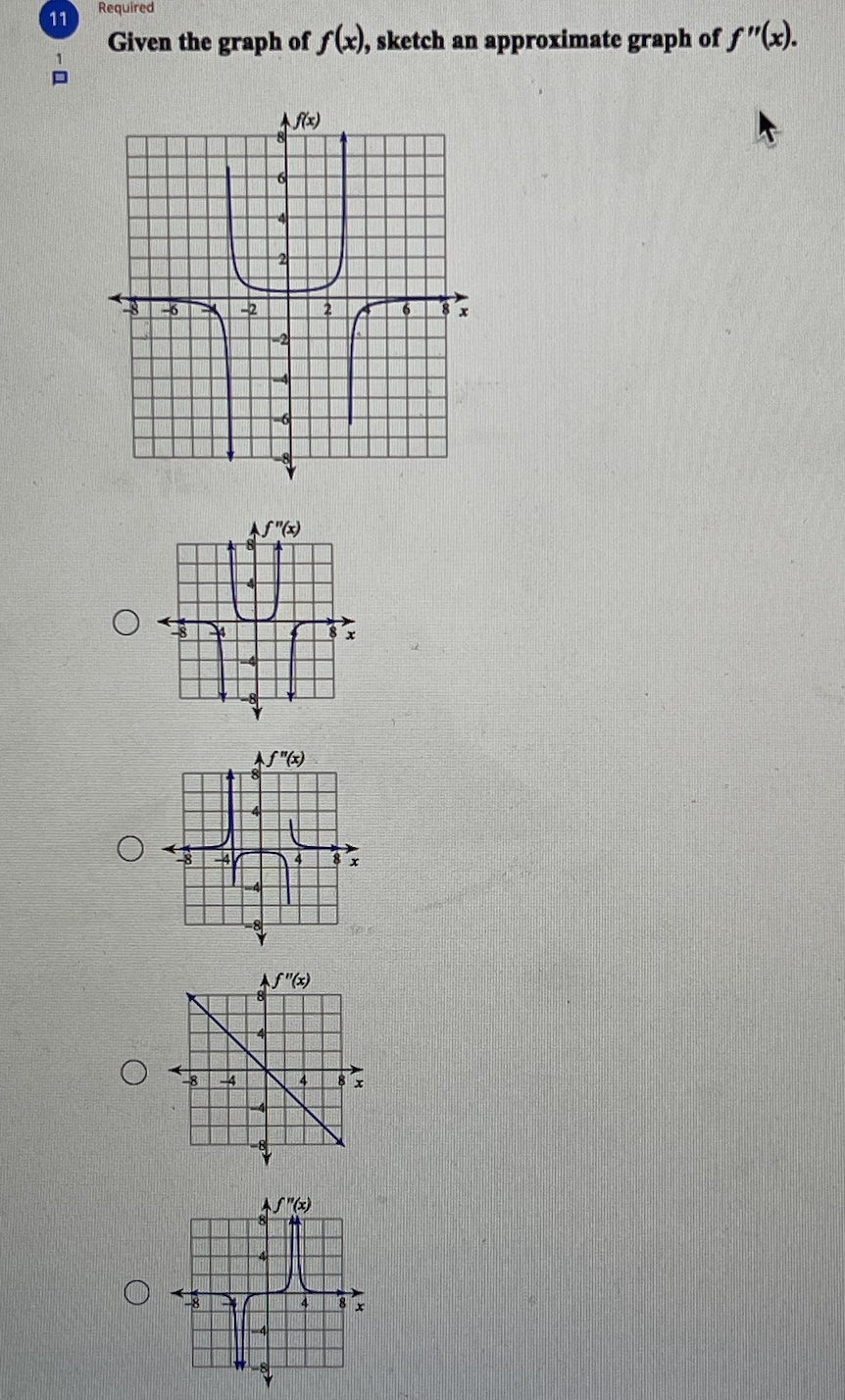
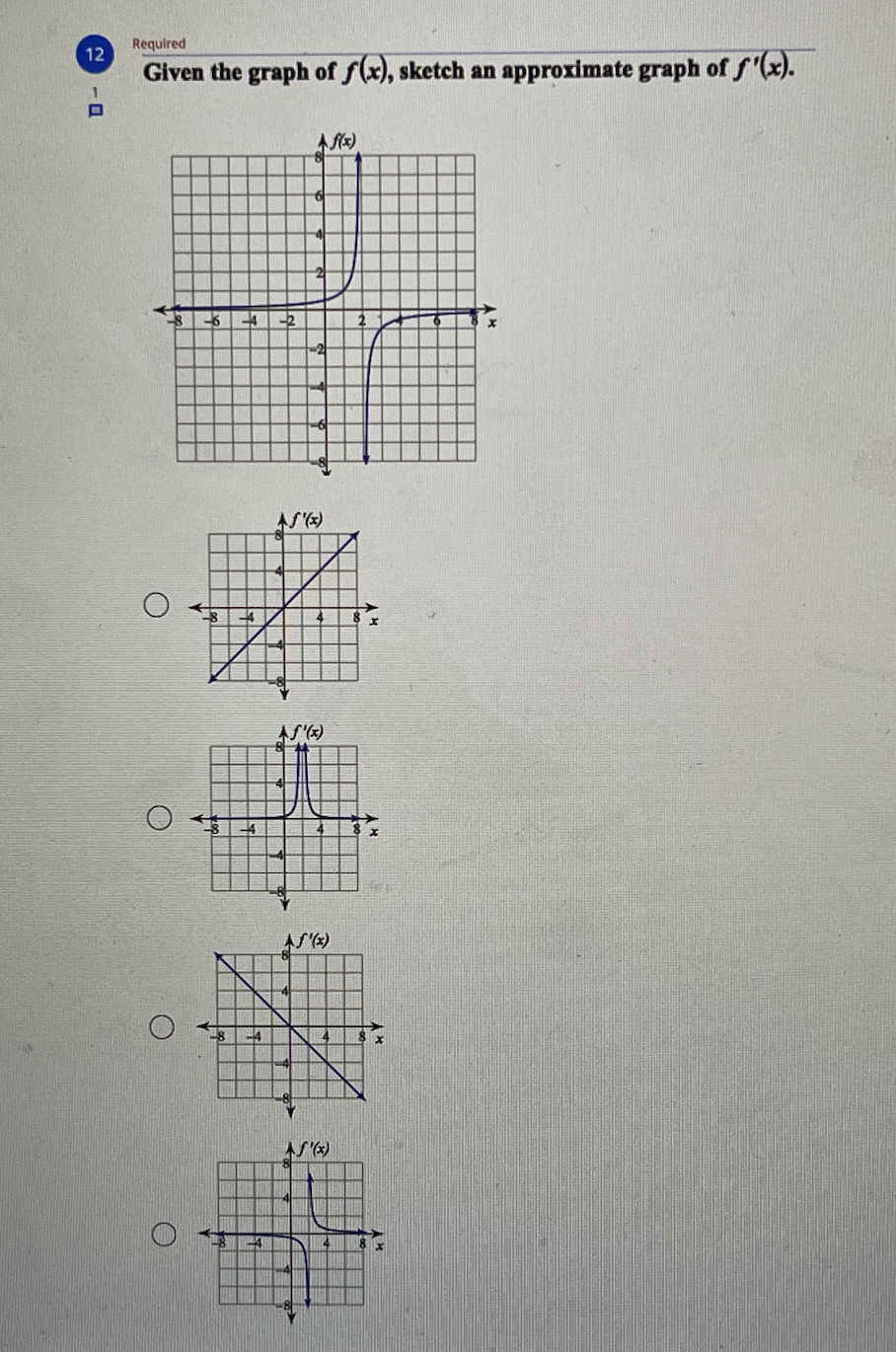
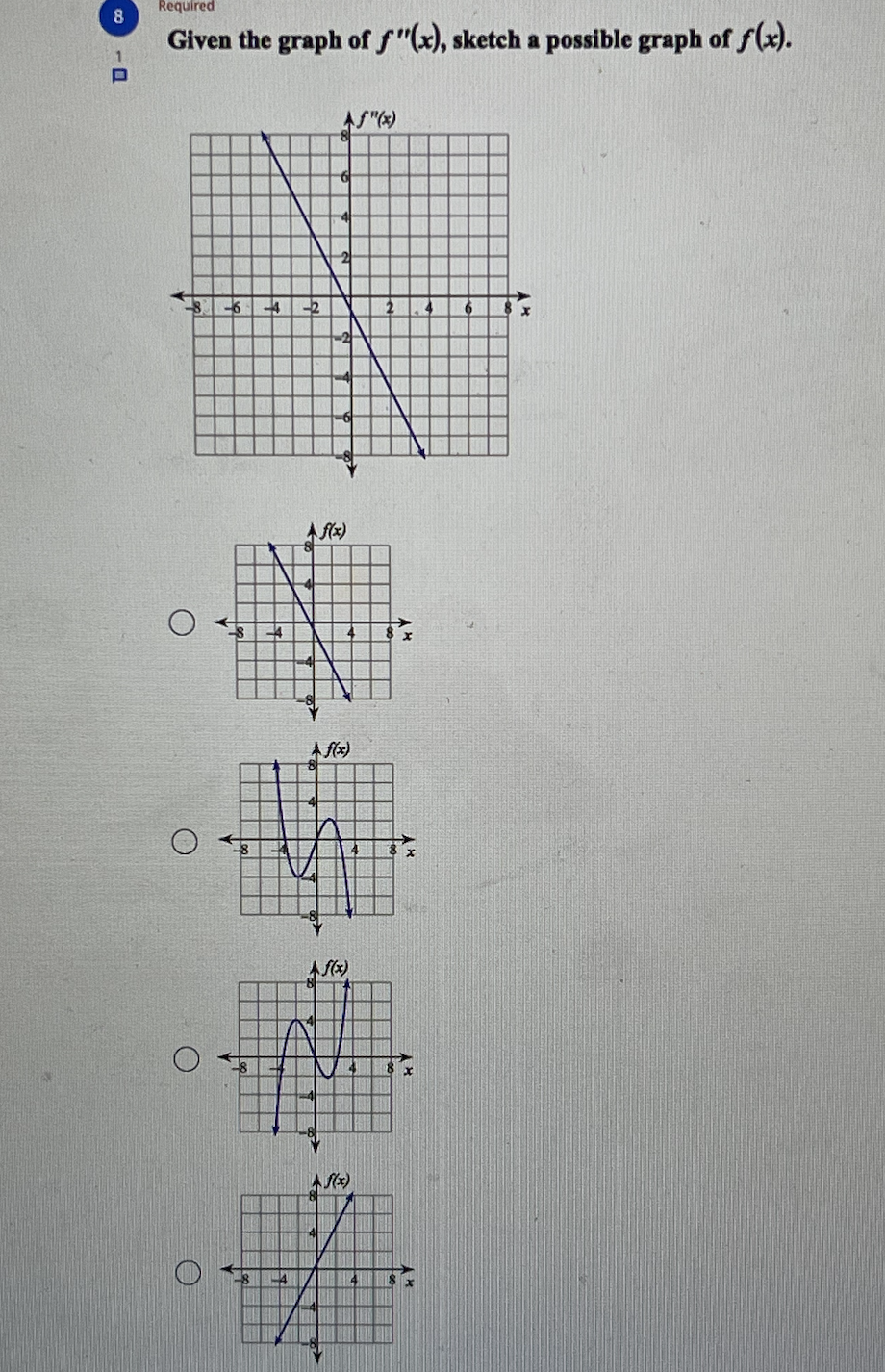
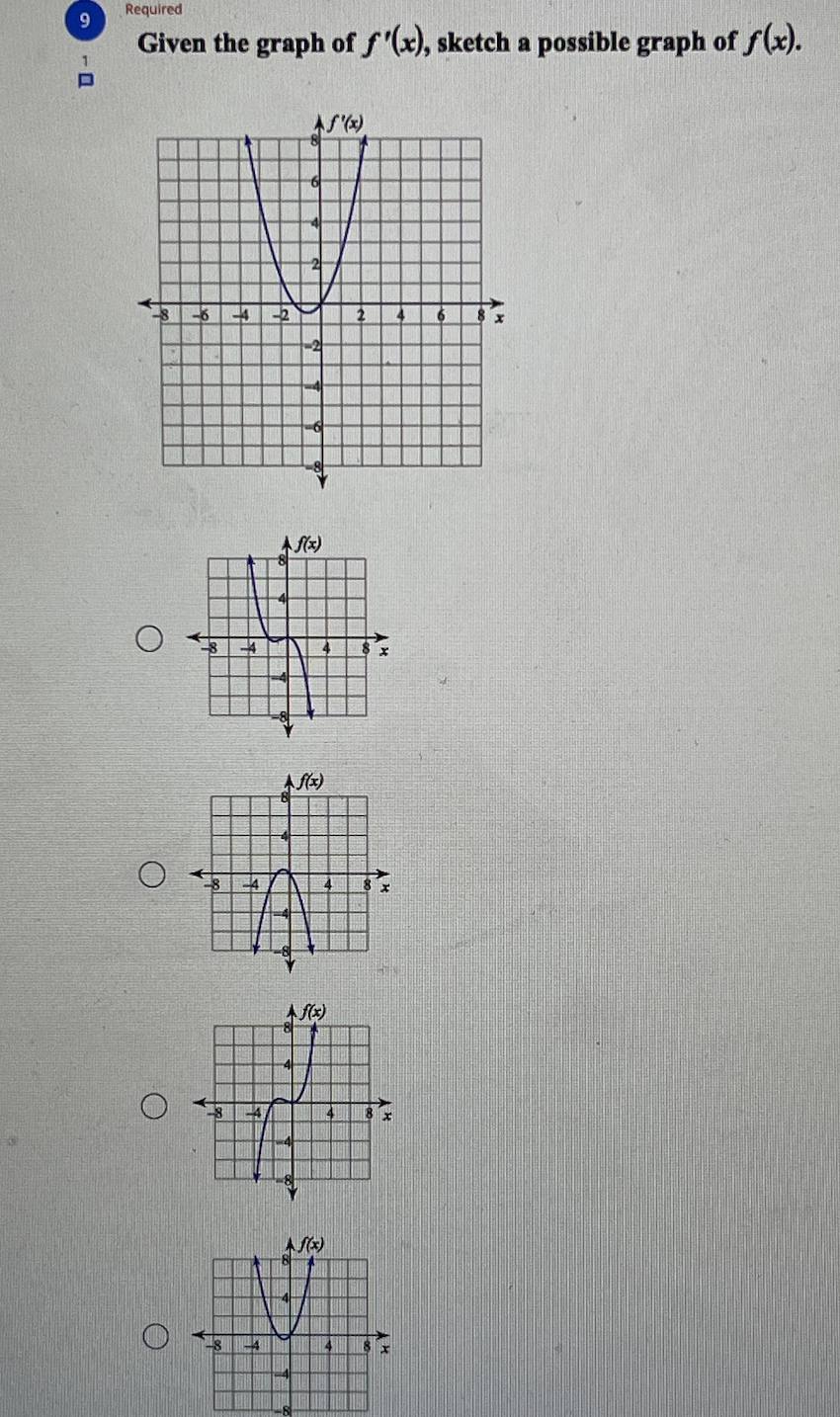
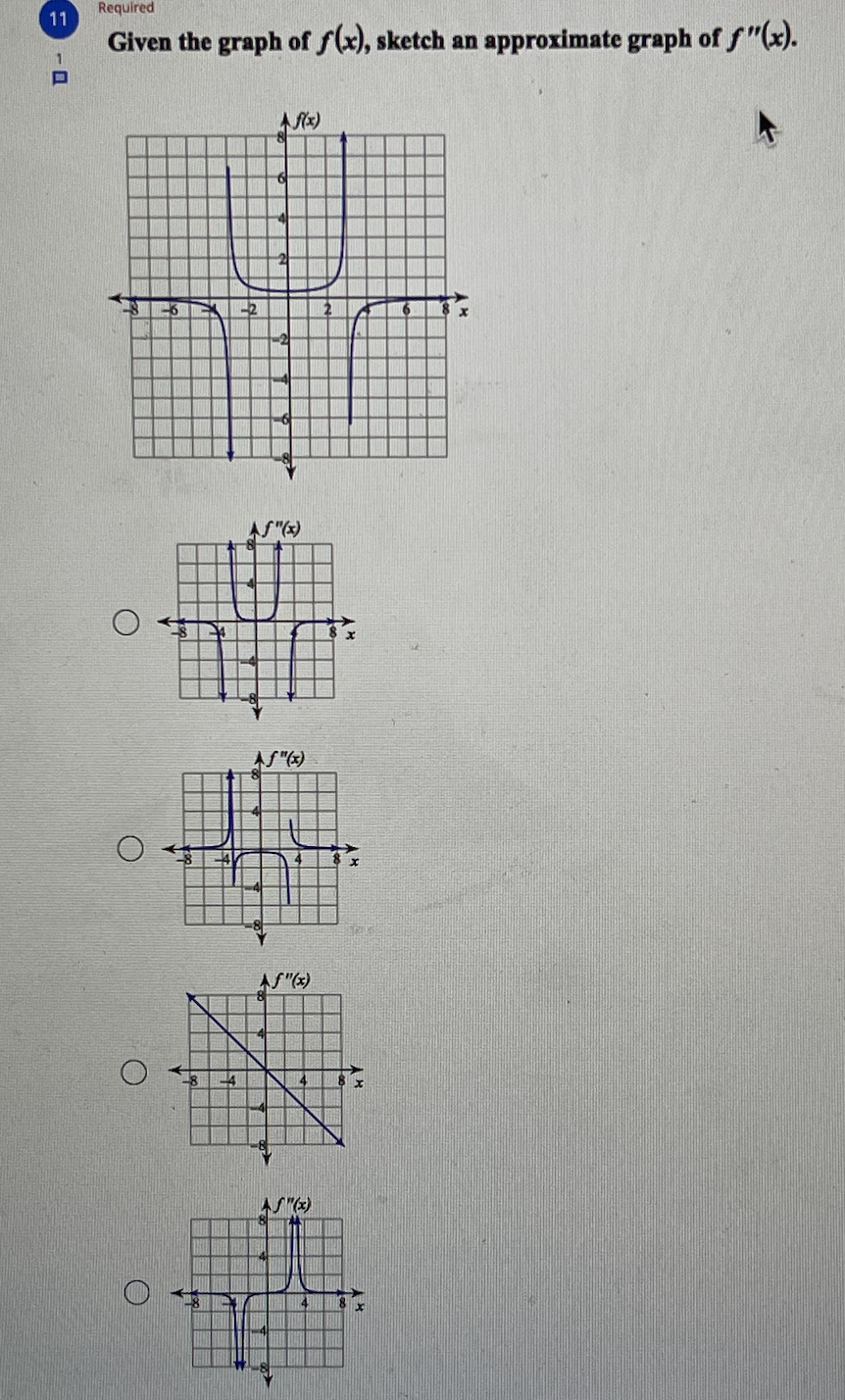
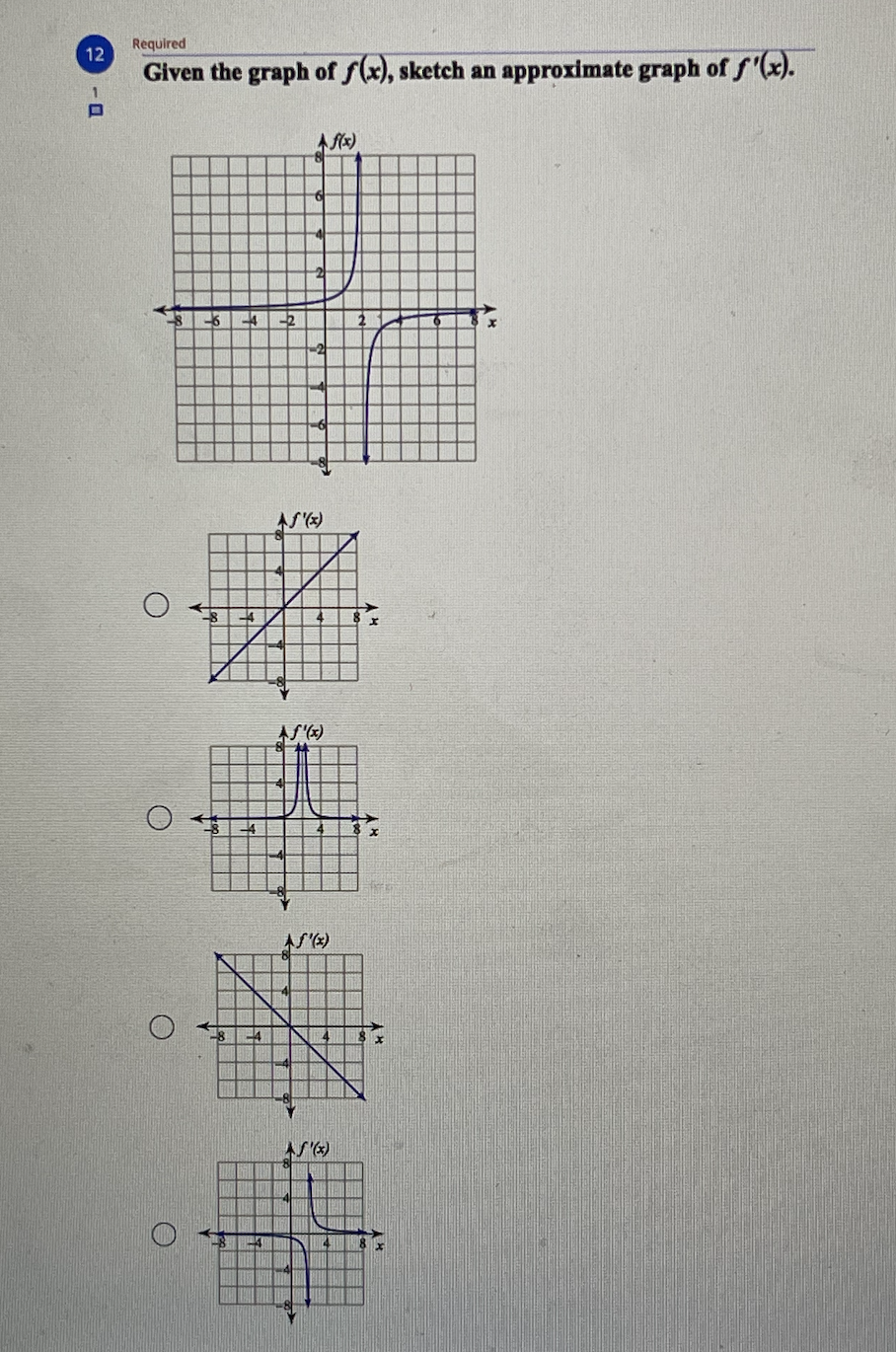
6 Required Find the open intervals where the function is concave up and concave down. y = x- - 1 Concave up: (-1, 1) Concave down: (-0., -1), (1, 0.) Concave up: 3' e down: (-0., - 4). (3. . ) Concave up: (-co, -4), (4, oo) Concave down: (-4, 4) O Concave up: (-co, -1), (1, co) Concave down: (-1, 1)8 Required Given the graph of f"(x), sketch a possible graph of f(x). J - AS" ( *) 36 4 A f(x) O A f(x) O Af(x) O As ( x )\f10 Find all points of absolute minima and maxima on the given interval. y = x' - 3x2 + 5; [1, 3] Absolute minimum: (2, 1) O Absolute maximum: (3, 5) Absolute minimum: (2, 1) O Absolute maximum: (0, 5) O Absolute minimum: (2, 1) No absolute maxima. No absolute minima. O No absolute maxima.11 Required 1 Given the graph of f(x), sketch an approximate graph of f"(x). A f(x) 6 AS" ( x ) O AS" ( x ) O AS" ( x ) O AS " ( x)Required Given the graph of f(x), sketch an approximate graph of f'(x). Af(x) O AS' ( x ) O X O AS ( * )Required 13 Find the x-coordinates of all critical points and find the open intervals where the function is increasing and decreasing. y=-x'+3x2 +1 N Critical points at: x = W O IN Increasing: -00, 3 co Decreasing: W/N 3 Critical points at: x = 4, 8 Increasing: (4, 8) Decreasing: (-00, 4), (8, 0.) No critical points exist. O Increasing: (-0o, 0), (2, co) Decreasing: (0, 2) O Critical points at: x = 0, 2 Increasing: (0, 2) Decreasing: (-0, 0), (2, 0.)Required 14 Find all points of absolute minima and maxima on the given interval. f(x) =-x2 - 4x - 1; [-5, 1] Absolute minimum: (-2, 3) Absolute maximum: (1, -6) No absolute minima. No absolute maxima. Absolute minima: (-5, -6), (1, -6) O Absolute maximum: (-2, 3) Absolute minimum: (-2, 3) O No absolute maxima