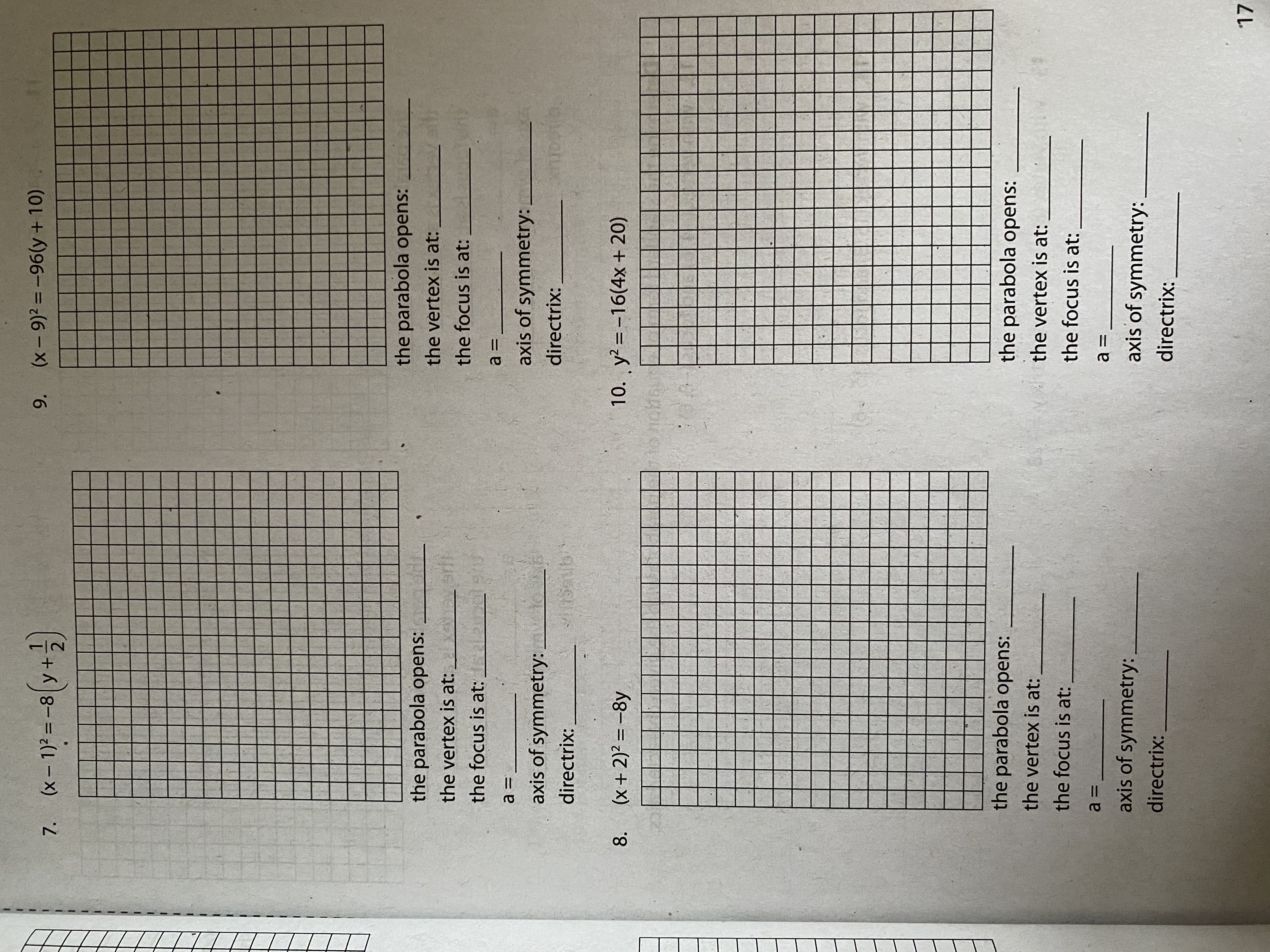
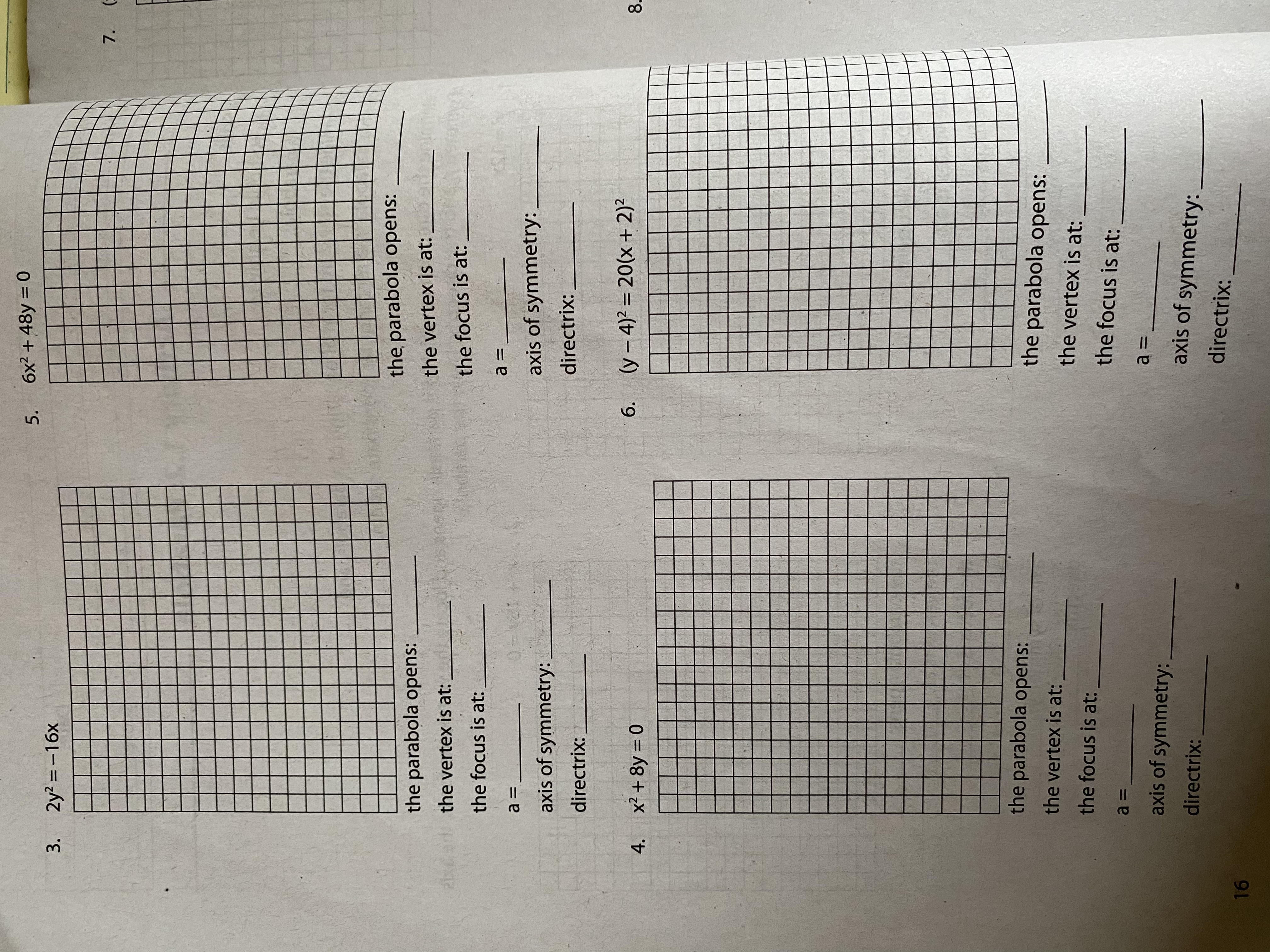
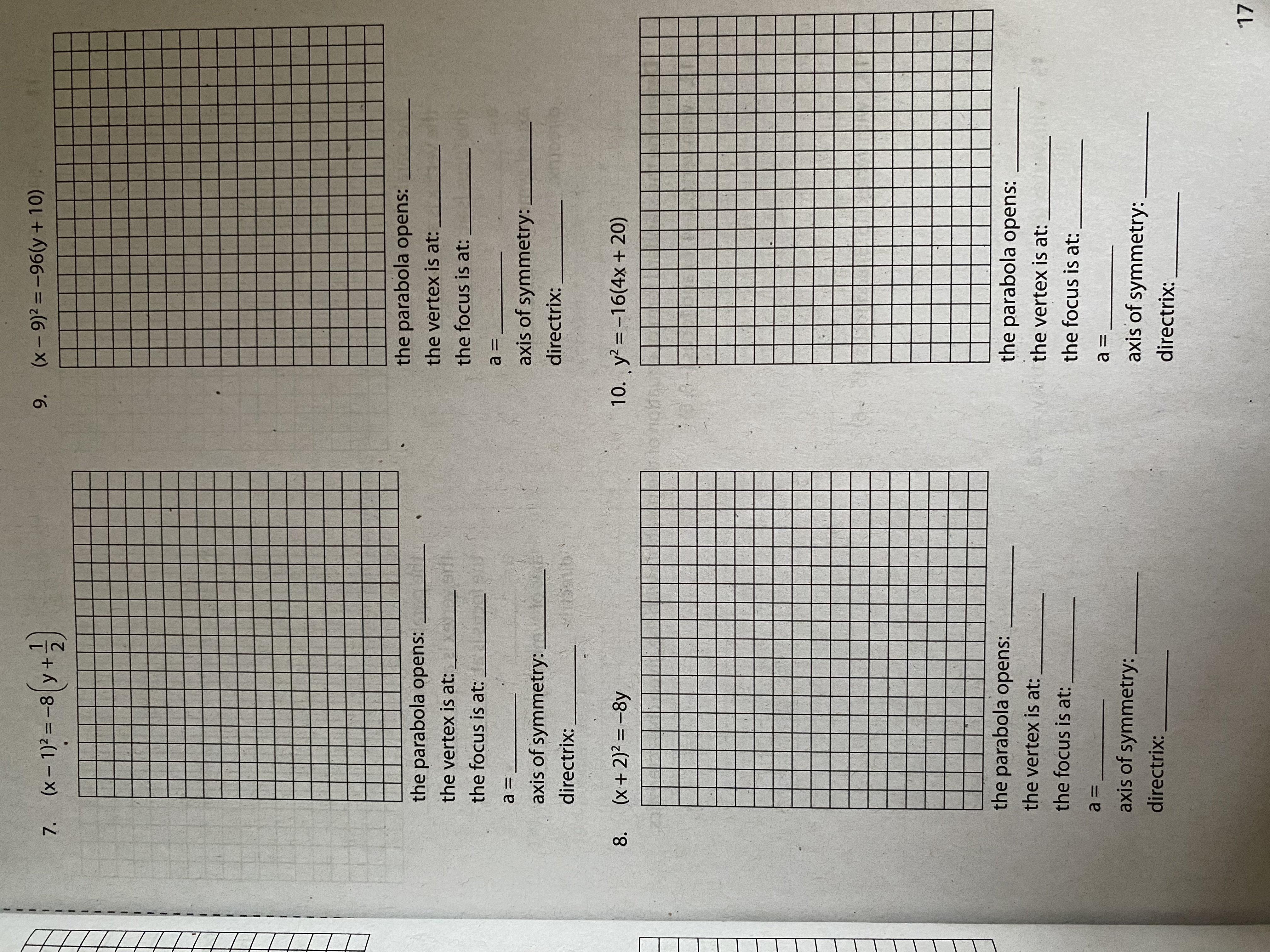
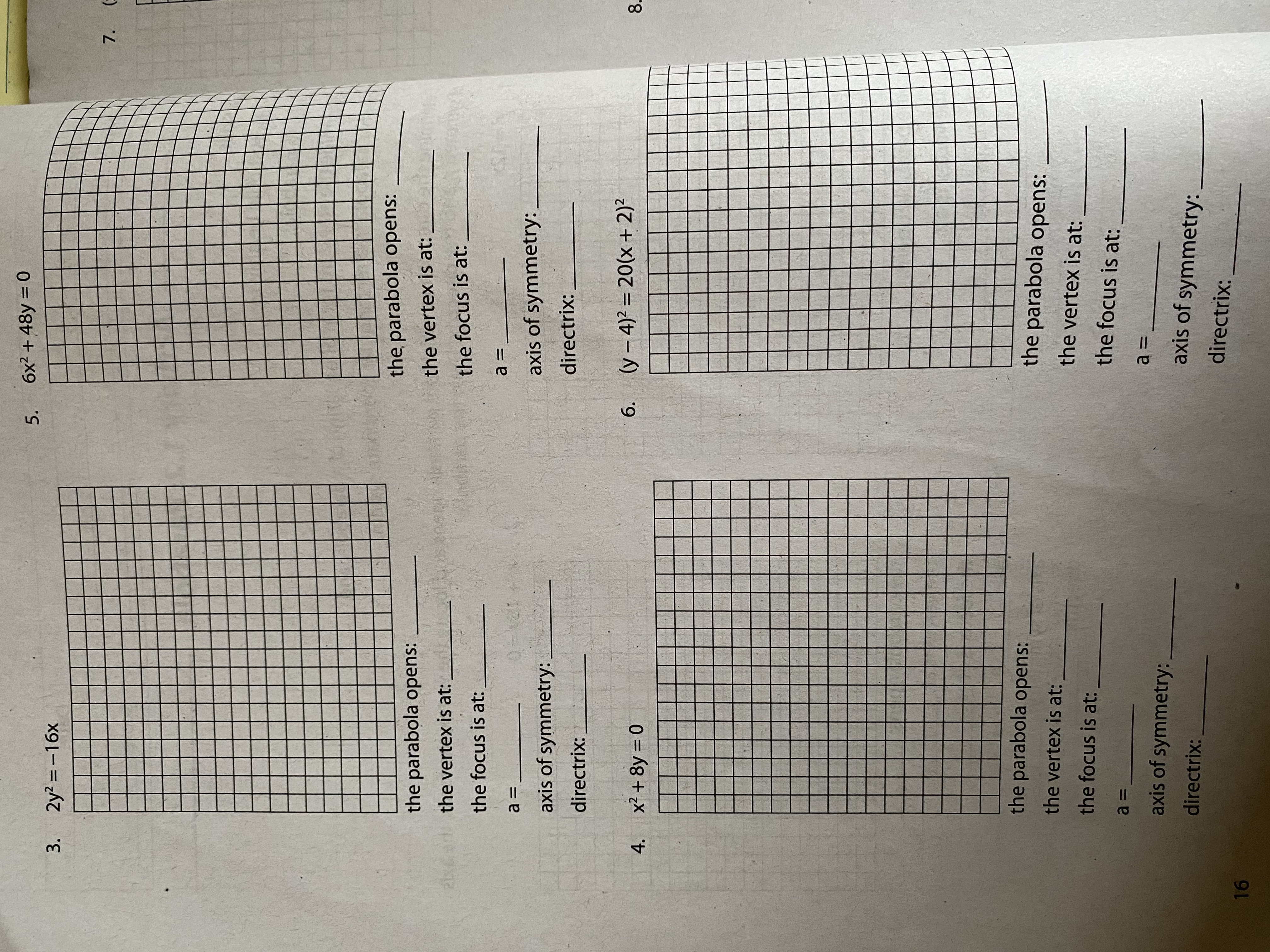
7. (x - 1)2 = -8(y+ 2 ) 9. (x - 9)2 =-96(y + 10) the parabola opens: the parabola opens: the vertex is at: the vertex is at: the focus is at: the focus is at: a = a = axis of symmetry: axis of symmetry: directrix: directrix: 8. ( x + 2) 2 =-8y 10. y2 = -16(4x + 20) the parabola opens: the parabola opens: the vertex is at: the vertex is at: the focus is at: the focus is at: a = a = axis of symmetry: axis of symmetry: directrix: directrix: 175. 6x2 + 48y = 0 3. 2y2 = -16x 7. the parabola opens: the parabola opens: the vertex is at:_ the vertex is at: the focus is at: the focus is at: a = a = axis of symmetry: axis of symmetry: directrix: directrix: 4. x2 + 8y = 0 6. (y - 4)2 = 20(x + 2)2 the parabola opens: the vertex is at: the parabola opens: the focus is at: the vertex is at: a = the focus is at: axis of symmetry: a = directrix: axis of symmetry: directrix: 16A. Determine the direction in which the parabola opens and locate the vertex, the focus, the axis of symmetry, and the directrix. Draw the parabola. 1. y2 = 12x 2. x2 + 16y = 0 the parabola opens: the parabola opens: the vertex is at: the vertex is at: the focus is at: the focus is at: a = a = axis of symmetry: axis of symmetry: directrix: directrix