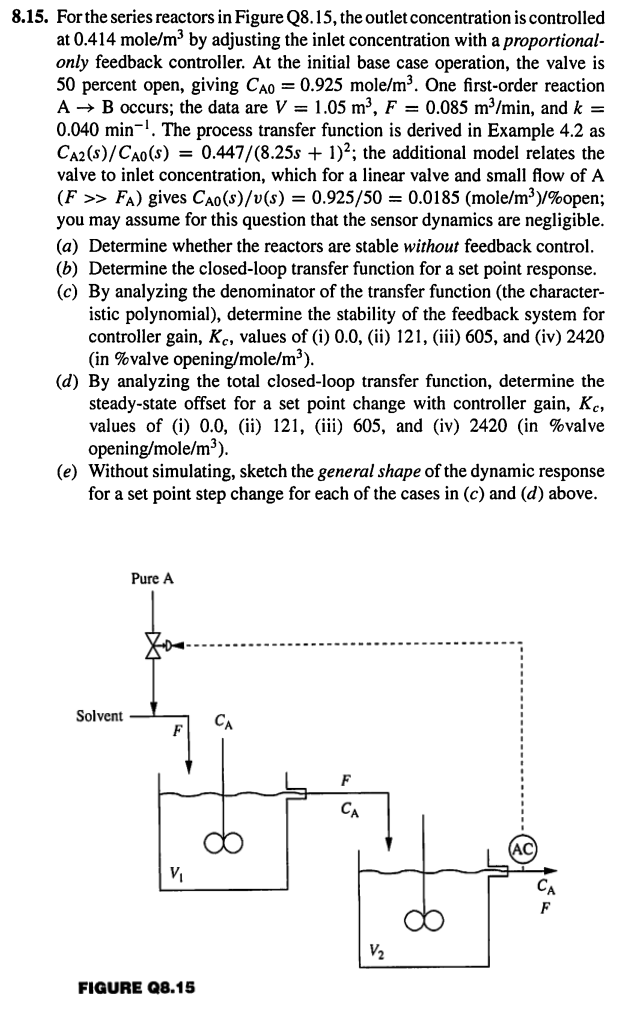
Question: 8 . 1 5 . For the series reactors in Figure Q 8 . 1 5 , the outlet concentration is controlled at 0 .
For the series reactors in Figure Q the outlet concentration is controlled
at mol by adjusting the inlet concentration with a proportional
only feedback controller. At the initial base case operation, the valve is
percent open, giving mol One firstorder reaction
B occurs; the data are and
The process transfer function is derived in Example as
; the additional model relates the
valve to inlet concentration, which for a linear valve and small flow of
gives open;
you may assume for this question that the sensor dynamics are negligible.
a Determine whether the reactors are stable without feedback control.
b Determine the closedloop transfer function for a set point response.
c By analyzing the denominator of the transfer function the character
istic polynomial determine the stability of the feedback system for
controller gain, values of iiiiii and iv
in valve opening
d By analyzing the total closedloop transfer function, determine the
steadystate offset for a set point change with controller gain,
values of iiiiii and ivin valve
opening
e Without simulating, sketch the general shape of the dynamic response
for a set point step change for each of the cases in and above.
FIGURE Q For the series reactors in Figure Q the outlet concentration is controlled
at molem by adjusting the inlet concentration with a proportionalonly feedback controller. At the initial base case operation, the valve is
percent open, giving Cao molem One firstorder reaction
A B occurs; the data are V m F mmin and k
min The process transfer function is derived in Example as
CAsCAs l; the additional model relates the
valve to inlet concentration, which for a linear valve and small flow of A
F FA gives CAsvsmolemopen;
you may assume for this question that the sensor dynamics are negligible.
a Determine whether the reactors are stable without feedback control.
b Determine the closedloop transfer function for a set point response.
c By analyzing the denominator of the transfer function the character
istic polynomial determine the stability of the feedback system for
controller gain, Kc values of iiiiii and iv
in valve openingmolem
d By analyzing the total closedloop transfer function, determine the
steadystate offset for a set point change with controller gain, Kc
values of iiiiii and ivin valve
openingmolem
e Without simulating, sketch the general shape of the dynamic response
for a set point step change for each of the cases in c and d above.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


