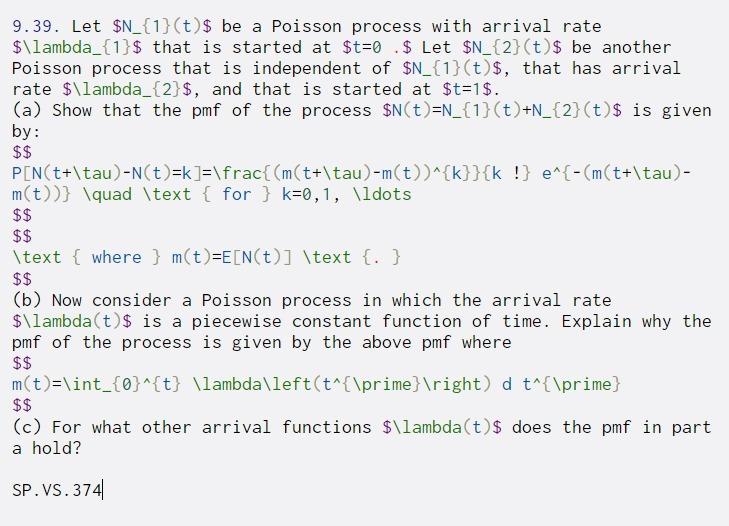
9.39. Let $N_{1}(t)$ be a Poisson process with arrival rate $\lambda_{1}$ that is started at $t=0 $ Let $N_{2}(t) $ be another Poisson process that is independent of $N_{1}(t)$, that has arrival rate $\lambda_{2}$, and that is started at $t=1$. (a) Show that the pmf of the process $N(t)=N_{1}(t)+N_{2}(t) $ is given by: $$ PIN(t+\tau)-N(t)=k]=\frac{(m(t+\tau)-m(t))^{k}}{k !) e^{-(m(t+\tau) - m(t))} \quad \text { for } k=0,1, \ldots $$ $$ \text { where } m(t)=E[N(t)] \text {. } $$ (b) Now consider a Poisson process in which the arrival rate $\lambda(t)$ is a piecewise constant function of time. Explain why the pmf of the process is given by the above pmf where $$ m(t)=\int_{0}^{t} \lambda\left(t^{\prime} ight) d t^{\prime} $$ (c) For what other arrival functions $\lambda(t) $ does the pmf in part a hold? SP.VS.374